2015-03-22
711
Получим формулы для определения нормальной и продольной силы, а также момента тангажа относительно вершины для конуса, обтекаемого идеальной жидкостью. В этом случае на поверхность тела действуют только силы аэродинамического давления.
Выделим на поверхности тела элементарную площадку: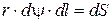 
(рис. 9.9). Нормальная сила, действующая на эту площадку, равна
.
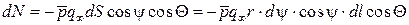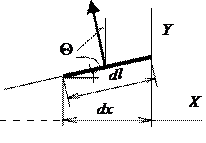
Рис. 9.9. Определение нормальной и продольной силы
Так как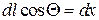 
, после интегрирования в пределах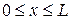 
(
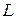– длина тела вращения) и 
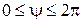получим выражение для нормальной силы, действующей на всю поверхность тела:
.
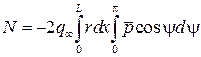Коэффициент нормальной силы равен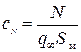 
, где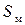 
– площадь миделевого сечения тела. Перейдем к безразмерным величинам и сделаем следующие замены: 
, 
, 
(
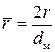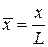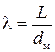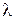– удлинение тела; 
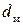– диаметр миделя). Тогда выражение для коэффициента нормальной силы примет вид
,
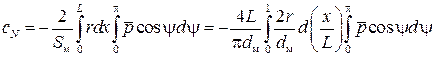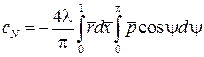. (9.12)
Аналогично получим формулу для коэффициента продольной силы. Элементарная продольная сила равна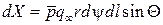 
. Так как 
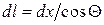, то
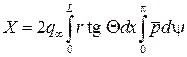и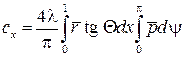 
. (9.13)
Формулы (9.12) и (9.13) применимы для любого тела вращения. Для конуса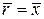 
, 
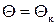и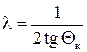 
. Тогда из формул (9.12) и (9.13) получим следующее:
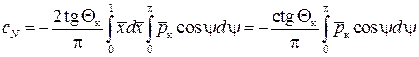, (9.14)
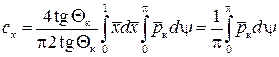. (9.15)
Коэффициент давления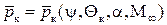 
. Коэффициент момента относительно вершины конуса, отнесенный к длине конуса 
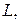равен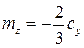 
. Из формул (9.14) и (9.15) следует, что коэффициенты 
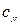и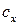 
зависят от углов атаки 
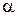, полураствора конуса 
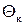и числа Маха 
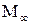, т. е. 
.
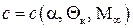Анализ результатов экспериментов и расчетов для конусов показывает, что при увеличении 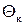коэффициент нормальной силы уменьшается, а коэффициент продольной силы увеличивается. Подобное противоположное влияние на эти аэродинамические коэффициенты оказывает число Маха: с увеличением числа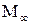 
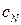увеличивается, а 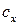уменьшается.
