Рассмотрим обтекание тонкого удлиненного тела вращения при малом угле атаке. В этом случае возмущенный поток в окрестности тела мало отличается от невозмущенного. По методу малых возмущений потенциал скорости потока удовлетворяет линейному дифференциальному уравнению и может быть представлен в виде суммы трех составляющих (рис. 9.10):
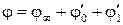 ,
,
где 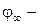 потенциал невозмущенного потока;
потенциал невозмущенного потока; 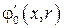 – потенциал скорости возмущения при осесимметричном
– потенциал скорости возмущения при осесимметричном 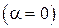 обтекании тела потоком со скоростью
обтекании тела потоком со скоростью 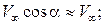
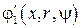 – потенциал, возникающий при поперечном обтекании тела потоком со скоростью
– потенциал, возникающий при поперечном обтекании тела потоком со скоростью 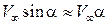 .
.
Согласно линейной теории потенциал обтекания тонкого тела при сверхзвуковых скоростях описывается уравнением
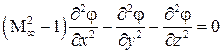 .
.
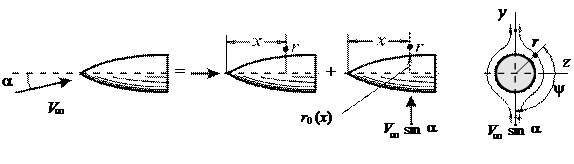 |
а б в
Рис. 9.10. Тонкое тело вращения при малом угле атаки:
а – 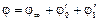 ; б –
; б – 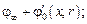 в –
в – 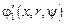
В безразмерных координатах (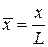 ,
, 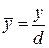 и
и 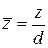 , где
, где 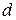 – диаметр миделевого сечения;
– диаметр миделевого сечения; 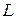 – длина тела) уравнение для потенциала перепишется в виде
– длина тела) уравнение для потенциала перепишется в виде
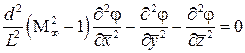 . (9.16)
. (9.16)
Для тонких тел 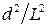 << 1, и, пренебрегая первым слагаемым в выражении (9.16) ввиду его малости, запишем следующее:
<< 1, и, пренебрегая первым слагаемым в выражении (9.16) ввиду его малости, запишем следующее:
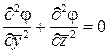 . (9.17)
. (9.17)
Уравнение (9.17) есть ни что иное, как уравнение Лапласа – уравнение неразрывности для плоского потенциального течения несжимаемой жидкости. То есть поток в плоскости ZOY поперечного сечения тонкого тела можно считать двумерным, совпадающим с поперечным обтеканием цилиндра радиусом, равным местному радиусу тела вращения 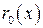 , несжимаемой жидкостью. Кроме того, из уравнения (9.17) следует также, что потенциал обтекания тонкого тела не зависит от числа
, несжимаемой жидкостью. Кроме того, из уравнения (9.17) следует также, что потенциал обтекания тонкого тела не зависит от числа 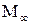 .
.
В результате некоторых преобразований уравнения (9.17) и интегрирования по углу 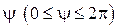 получим выражение для нормальной силы, действующей на элемент тела вращения длиной
получим выражение для нормальной силы, действующей на элемент тела вращения длиной  :
:
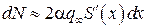 , (9.18)
, (9.18)
где 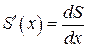 . Отсюда следует, что нормальная сила
. Отсюда следует, что нормальная сила 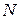 появляется только на участках с переменной площадью поперечного сечения. Знак силы зависит от знака производной
появляется только на участках с переменной площадью поперечного сечения. Знак силы зависит от знака производной 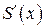 (рис. 9.11).
(рис. 9.11).
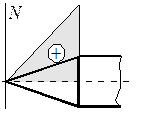
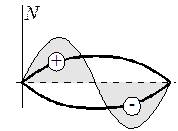
а б
Рис. 9.11. Распределение нормальной силы по поверхности конуса:
а – цилиндрического тела; б – параболического тела
Носовая часть корпуса 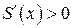 создает положительную нормальную силу, а суживающаяся хвостовая часть
создает положительную нормальную силу, а суживающаяся хвостовая часть 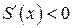 – отрицательную нормальную силу, тогда как цилиндрический отсек, для которого
– отрицательную нормальную силу, тогда как цилиндрический отсек, для которого 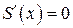 , при обтекании тела идеальной жидкостью не создает нормальной силы.
, при обтекании тела идеальной жидкостью не создает нормальной силы.
Нормальная суммарная сила для тонкого тела вращения равна
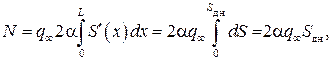
а коэффициент нормальной силы равен
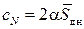 , (9.19)
, (9.19)
где 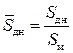 – относительная площадь донного среза (угол
– относительная площадь донного среза (угол 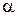 измеряется в радианах). Для носовой части
измеряется в радианах). Для носовой части 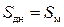 и
и 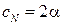 независимо от формы носовой части и числа Маха.
независимо от формы носовой части и числа Маха.
 Момент элементарной нормальной силы относительно вершины тела (рис. 9.12) – момент тангажа – равен
Момент элементарной нормальной силы относительно вершины тела (рис. 9.12) – момент тангажа – равен 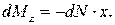 Знак «минус» в этой формуле говорит о том, что создаваемый момент – это момент на пикирование:
Знак «минус» в этой формуле говорит о том, что создаваемый момент – это момент на пикирование:
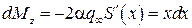 ,
,
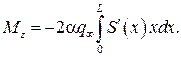
Коэффициент момента равен
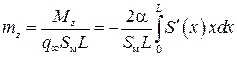 ,
,
т. е. 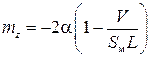 , где
, где 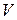 – объем носовой части.
– объем носовой части.
 2015-03-22
2015-03-22 773
773








