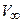2015-03-22
1230
При сверхзвуковом обтекании конуса под углом атаки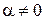 
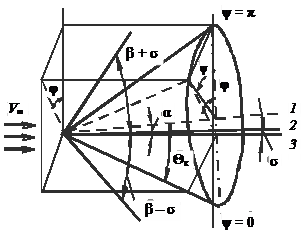
поток около него будет обладать свойством конического течения с той особенностью, что параметры сохраняют постоянное значение не целиком на конической поверхности, а вдоль отдельных прямолинейных образующих конуса. Параметры газа в таком потоке изменяются при переходе от одной образующей, проходящей через вершину конуса, к другой. Такой конический поток обычно рассматривают в сферической системе координат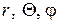 
(рис. 9.5), выбранной таким образом, что координате 
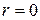соответствует вершина конуса, оси координат 
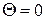(ось 3) – направление скорости набегающего потока, а меридиональной плоскости 
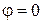– плоскость, проходящая через ось 3 и ось 1, т. е. ось симметрии конуса. В этой системе координат уравнение конуса, наклоненного к оси 3 под углом 
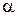(на рис. 9.5 этот угол отрицательный), будет следующим:
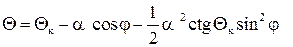, (9.8)
где 
– сферическая координата для образующей конуса. Для подветренной образующей 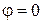, а для наветренной –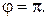 
 |
|
Из свойств конического потока следует, что значения его параметров не зависят от r, а являются функциями переменных 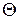и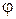 
. Поэтому в уравнениях возмущенного течения отсутствуют производные по r. В случае несимметричного конического сверхзвукового потока течение в плоскости 
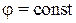будет изоэнтропическим. Это объясняется тем, что вдоль линии пересечения этой плоскости с поверхностью скачка, представляющей собой прямую линию, энтропия будет постоянной, так как условия перехода газа через скачок одинаковы для каждой линии тока. Такое же явление будет наблюдаться в любой другой плоскости 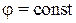. Однако в связи с тем, что угол наклона скачка 
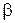неодинаков в каждой из этих плоскостей, неодинаковой будет и энтропия, являющаяся, таким образом, функцией угла 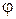. Из этого следует, что в целом несимметричный конический поток за скачком оказывается неизоэнтропическим.
Теоретической основой для исследования такого потока являются уравнения движения идеальной среды и уравнение неразрывности в сферической системе координат. Решения системы дифференциальных уравнений находят в виде
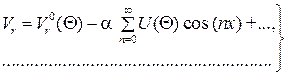(9.9)
Аналогичные выражения записывают и для остальных искомых параметров: составляющих скорости по соответствующим направлениям сферической системы координат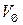 
и 
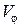, давления 
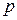, плотности 
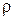, где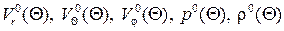 
– это параметры симметричного обтекания на конусе с углом .
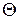Каждое из уравнений (9.9) представляет собой ряд, в котором член, линейный по отношению к углу атаки, определяет решение в первом приближении, а квадратичный член – во втором. При малых углах 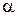значения параметров будут мало отличаться от соответствующих значений при симметричном обтекании, и влияние угла 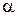достаточно учесть только линейными членами. С возрастанием 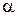возникает необходимость вести расчет с учетом второго приближения, которым обычно и ограничиваются, полагая, что углы атаки невелики (что справедливо для баллистических ракет и ракет-носителей).
Из выражений (9.9) следует, что определение параметров обтекания конуса под углом атаки начинается с решения частной задачи о симметричном потоке около того же конуса. В результате ее решения отыскиваются значения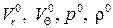 
в зависимости от угла 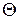. Далее рассматривается влияние угла атаки.
Задача о влиянии угла атаки в первом приближении сводится к определению коэффициентов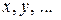 
рядов (9.9) при условии, что квадратичные и более высокие степени в них отсутствуют, при этом принимают n = 1. Тогда система (9.9) запишется следующим образом:
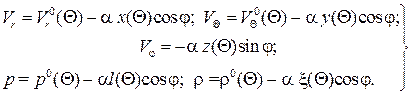(9.10)
В рассматриваемых уравнениях коэффициенты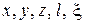 
можно рассматривать как величины, определяющие эффект угла атаки в первом приближении, а коэффициенты 
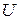и другие – во втором. Все эти коэффициенты зависят от одной переменной .
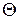Найденные в результате решения задачи коэффициенты x, y, z, отнесенные к максимальной скорости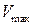 
, а также безразмерные величины 
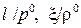просчитаны для различных углов конуса и чисел 
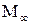и внесены в таблицы. При их помощи по формулам (9.10) ведется расчет скорости, давления и плотности численными методами (в аэродинамике наиболее развиты конечно-разностные методы) с помощью ЭВМ. Не вдаваясь в подробности расчетов, рассмотрим их результаты (рис. 9.6).
Рис. 9.6. Зависимости коэффициента давления:
а – от угла атаки; б – от угла ψ; в – от числа Маха
Простой логический анализ течения около конуса позволяет сделать вывод, что на его наветренной стороне (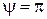
) давление должно быть больше, чем на подветренной. Это наглядно иллюстрируют приведенные качественные зависимости. С увеличением угла конуса давление возрастает на всей его поверхности. При малых углах атаки 
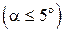коэффициент давления 
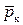практически линейно зависит от 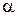(рис. 9.6, а). С увеличением числа Маха набегающего потока (рис. 9.6, в) коэффициент давления монотонно уменьшается во всех меридиональных плоскостях.
