На рисунке изображены фрагменты электрических схем, называемые соответственно треугольником (D) и звездой (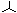 ).
).
Для эквивалентной замены одной схемы на другую необходимо сохранить величины токов 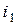 ,
, 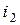 ,
, 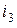 и напряжений
и напряжений 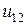 ,
, 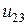 ,
, 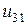 .
.
Рассмотрим преобразование соединения треугольником в соединение звездой. Данное преобразование должно обеспечивать эквивалентность исходной и преобразованной схем при любых режимах работы. Поэтому проанализируем режимы работы в упрощенных схемах.
Если ток 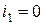 , то сопротивление между узлами 2 и 3 в каждой из схем должны быть равны между собой
, то сопротивление между узлами 2 и 3 в каждой из схем должны быть равны между собой
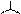
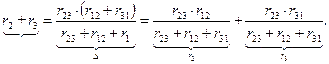
Аналогично, при 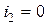 , получим
, получим
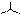
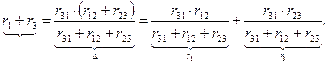
Выделяя справа от знака равенства одинаковые слагаемые, получим выражения, позволяющие рассчитать сопротивления звезды по известным сопротивлениям треугольника:
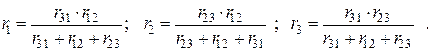
Рассмотрим преобразование соединения звездой в соединение треугольником.
Если напряжение 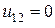 , то сопротивления между узлами 2 и 3 в каждой из схем одинаковы
, то сопротивления между узлами 2 и 3 в каждой из схем одинаковы
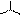
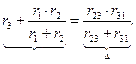
Записав обратные величины для левой и правой частей этого равенства, получим
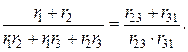
Отсюда следует
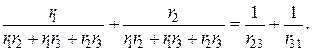 (*)
(*)
Аналогично, при 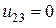 имеем
имеем
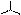
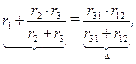
следовательно,
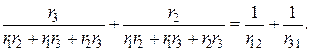 (**)
(**)
Сопоставляя соотношения (*) и (**), можем записать формулы для расчета сопротивлений треугольника по известным сопротивлениям звезды
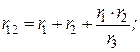
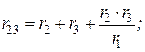
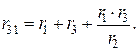
Пример. Найти эквивалентное сопротивление электрической цепи.
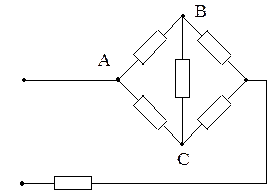
Данную схему не удается упростить с помощью последовательно- параллельных преобразований Используя преобразование треугольника АВС в звезду, можно получить эквивалентное сопротивление 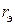 следующим образом
следующим образом
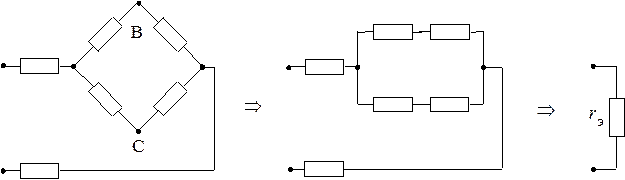
 2015-03-22
2015-03-22 644
644








