Решим следующую комбинаторную задачу.
Сколькими способами можно упорядочить 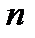 -множество
-множество 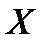 ?
?
Перестановками без повторений называют различные упорядоченные 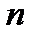 -множества, которые состоят из одних и тех же элементов, а отличаются друг от друга лишь порядком. Число таких перестановок обозначают
-множества, которые состоят из одних и тех же элементов, а отличаются друг от друга лишь порядком. Число таких перестановок обозначают 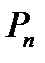 (от французского слова permutation – перестановка).
(от французского слова permutation – перестановка).
Формулу для 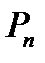 получаем из выражения (2) при
получаем из выражения (2) при 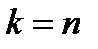 :
:
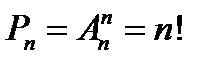 . (3)
. (3)
Пример 3. Сколькими способами можно посадить на скамейку 9 человек?
Ответ: 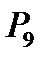 =9!=362880.
=9!=362880.
К перестановкам с повторениями приводит следующая задача.
Имеется 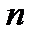 -множество
-множество 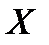 , состоящее из
, состоящее из 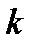 различных элементов (
различных элементов (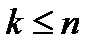 ). Сколько перестановок можно сделать из
). Сколько перестановок можно сделать из 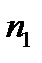 элементов первого типа,
элементов первого типа, 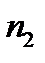 элементов второго типа,…,
элементов второго типа,…, 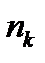 элементов
элементов 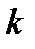 -го типа?
-го типа?
Перестановки элементов каждого типа можно делать независимо друг от друга. Поэтому по правилу произведения элементы множества можно переставлять друг с другом 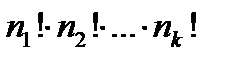 способами так, что перестановки не изменятся. Тогда число различных перестановок с повторениями буде равно
способами так, что перестановки не изменятся. Тогда число различных перестановок с повторениями буде равно
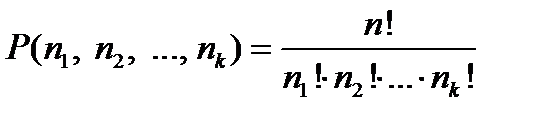 , (4)
, (4)
где 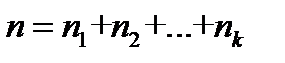 .
.
Пример 4. Сколько перестановок можно сделать из букв слова «Миссисипи»?
В данном случае 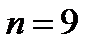 ,
, 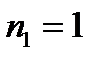 («М»),
(«М»), 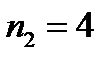 («и»),
(«и»), 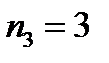 («с»),
(«с»), 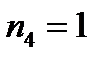 («п»). По формуле (4)
(«п»). По формуле (4)
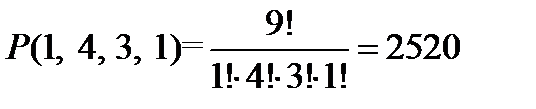 .
.
 2015-03-22
2015-03-22 574
574








