Решение.
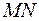 - средняя линия
- средняя линия 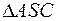 и по свойствам
и по свойствам 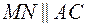 и
и 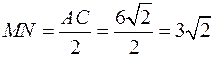 .
.
Отметим, что точка 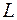 пересечения средней линии
пересечения средней линии 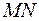 и высоты
и высоты 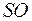 является серединой высоты, и, следовательно,
является серединой высоты, и, следовательно, 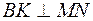 .
.
Через точку 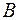 в плоскости основания
в плоскости основания 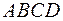 проведем прямую
проведем прямую 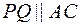 до пересечения с продолжением сторон
до пересечения с продолжением сторон 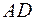 и
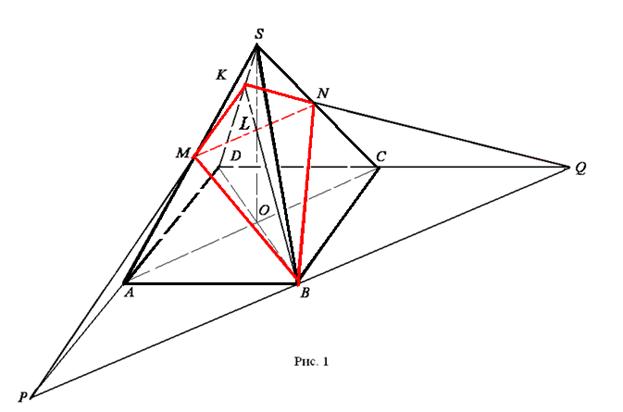
и 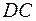 (Рис. 1). Следовательно,
(Рис. 1). Следовательно, 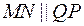 .
.
Проведем прямые 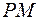 и
и 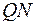 до пересечения с ребром
до пересечения с ребром 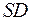 в некоторой точке
в некоторой точке 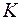 .
.
Сечение 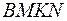 - искомое.
- искомое.
б) Площадь сечения подсчитаем по формуле: 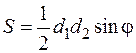 .
.
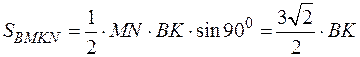 .
.
Вынесем сечение 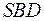 на отдельный чертеж (Рис. 2).
на отдельный чертеж (Рис. 2).
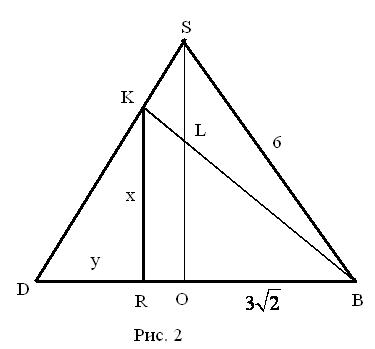
Пусть 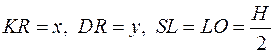 , где
, где 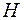 - высота пирамиды.
- высота пирамиды.
По теореме Пифагора: 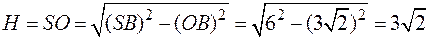 .
.
Из подобия треугольников 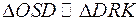 имеем:
имеем:
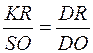 или
или 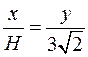 , откуда,
, откуда, 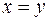 .
.
Из подобия треугольников 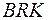 и
и 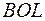 имеем:
имеем:
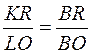 или
или 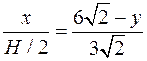 .
.
Решая полученную систему уравнений, находим 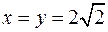 .
.
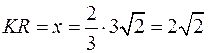 ,
, 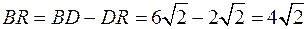 .
.
Из 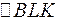 по теореме Пифагора имеем:
по теореме Пифагора имеем:
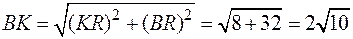 .
. 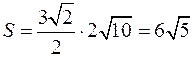 . Ответ:
. Ответ: 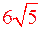
Пример 3.
На ребрах 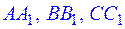 правильной треугольной призмы расположены точки
правильной треугольной призмы расположены точки 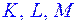 соответственно. Известно, что угол между прямыми
соответственно. Известно, что угол между прямыми 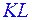 и
и 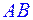 равен
равен 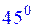 , а угол между прямыми
, а угол между прямыми 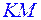 и
и 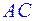 равен
равен 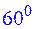 .
.
а) Построить сечение, проходящее через точки 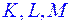 .
.
 2015-03-22
2015-03-22 699
699








