2015-03-22
464
Выходные данные:
Временной интервал T = 30 лет;
Число аварий на объекте за временной интервал Т, n = 2,5;
Временной интервал τ = 4 года;
Количество аварий N = 4.
Решение:
Для решения данной задачи используем формулу 5.4 дискретного распределения Пуассона
,
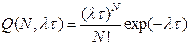где N = 0,1,2,… λτ > 0, а интенсивность отказов λ равна количеству аварий за год по статистике:
λ = n / T
Оценка риска аварии на объекте за период τ определяется с учетом формулы 5.3:
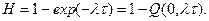
Тогда: λ = 2,5 / 30 = 0,083; λτ = 0,083 ∙ 4 = 0,33.
Имеем:
| N=1 | |
| Q(1;4∙0,08)= | 0,239 |
| 23,9% | |
| N=4 | |
| Q(4;4∙0,08)= | 0,00037 |
| 0,037% | |
| N=0 | |
| Q(0;0,08)= | 0,920 |
| 92% | |
| N=0 | |
| Q(0;4∙0,08)= | 0,717 |
| 71,7% | |
| H(4)= | 0,283 |
| 28,3% | |
| H(1)= | 0,08 |
| 8% |
Вероятность одной аварии на объекте в течение 4-х лет
Вероятность четырех аварии на объекте в течение 4-х лет
Вероятность безаварийного функционирования объекта в течение 1 года
Вероятность безаварийного функционирования объекта в течение 4-х лет
Оценка риска аварийности для 4-х лет
Оценка риска аварийности для 1-го года
