Метод гармонической линеаризации

Рассмотрим на примере конкретной системы

e

g

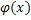
Wрег(р)

Wo(p)

x

u

y

-

Предположим, что на вход нелинейного звена поступает гармонический сигнал .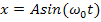

Нелинейность имеет вид:

Q

a

-b b х

-a

Рис.1

На выходе будет:

Q u

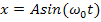
b

t₁ t₂ T t₃ t

ψ₁ π ψ₂ 2π ψ₃ ψ

-b

-Q

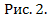
Как видно, на выходе нелинейного звена получились прямоугольные 2-полярные колебания с периодом, равным Т.

Такие колебания, очевидно, можно представить с помощью ряда Фурье:

,

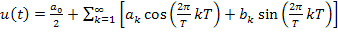Где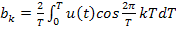

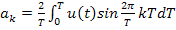
Если линейная часть является инерционной системой с убывающей амплитудно-частотной характеристикой, то высшие гармоники сглаживаются линейной частью (имеем фильтр, т.к. убывающая амплитудная характеристика соответствует фильтру высоких частот). В этом случае в качестве выхода нелинейного звена можно рассматривать только первую гармонику, т.к. остальные все равно будут сглажены линейной частью.

Тогда .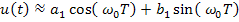

В связи с тем, что вид колебаний на выходе нелинейного звена зависит от амплитуды входного колебания, коэффициенты 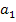, 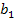определяются амплитудой входного сигнала.

Введем новые коэффициенты:

, .

,

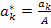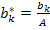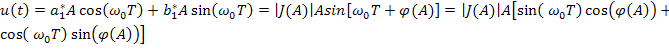где ,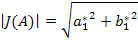

,

,

,

.

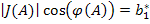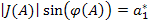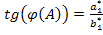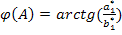Имеем некоторую характеристику нелинейного звена 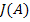, которая является аналогом частотной характеристики линейного звена, поскольку она изменяет амплитуду и фазу входного гармонического сигнала, не изменяя частоты. Но зависит эта характеристика не от частоты колебаний, а от амплитуды.

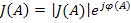
Фактически нелинейная система была сведена к линейной (линеаризована), и характеристика нелинейного звена равна .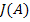

Как известно, в замкнутой линейной системе возникают колебания в случае, когда комплексная частотная характеристика разомкнутой системы проходит через точку 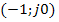(при устойчивой линейной части), т.е.:

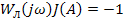
Если это комплексное уравнение имеет действительные корни 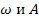, то в замкнутой нелинейной системе возникают автоколебания.

Решают уравнение либо численно, сведя его к 2-м скалярным уравнениям:

,

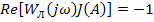
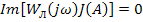либо графически, представив в виде 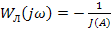, называемом уравнением Гольдфарба:

Im

Re

W_Л(jω) -1/J(A)

Точки пересечения графиков дают корни уравнения A и ω.

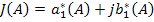- эквивалентная частотная характеристика (эквивалентная передаточная функция) получается для конкретной статической характеристики нелинейности (см. рис.1) и выхода нелинейного звена u(t) (рис.2) из коэффициентов ряда Фурье следующим путем:

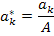
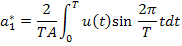
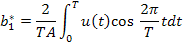
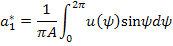
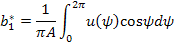
Чтобы упростить интеграл, рассмотрим интервал 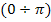. Тогда

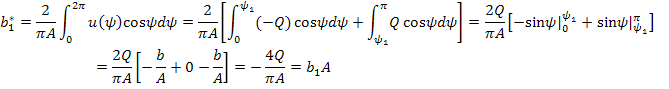
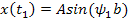
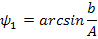
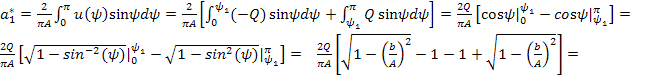
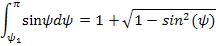
Разбивая интеграл 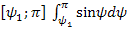на участки: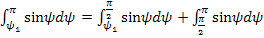

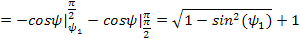
Тогда

.

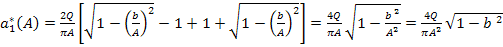Как видно, .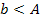

Определив коэффициенты ряда Фурье, необходимо найти значение уравнения:

.

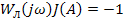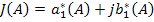, т.е. определить значения 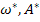, которые преобразуют уравнение в тождество, для чего уравнение можно разделить на скалярные:

,

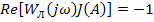
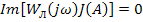и найти все решения.