| V1 | Определение сходимости ряда: |
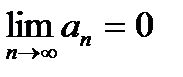
| |
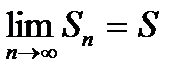
| |
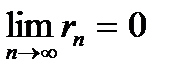
| |
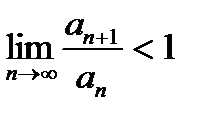
| |
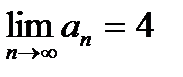
| |
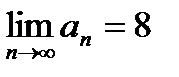
|
Вопрос №34
| V1 | Достаточный признак сходимости Даламбера: |
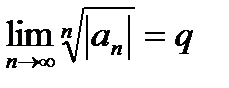 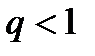 . .
| |
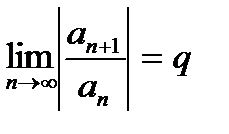 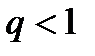 . .
| |
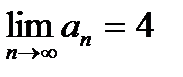
| |
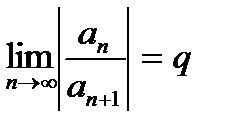 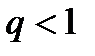 . .
| |
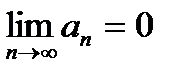 . .
| |
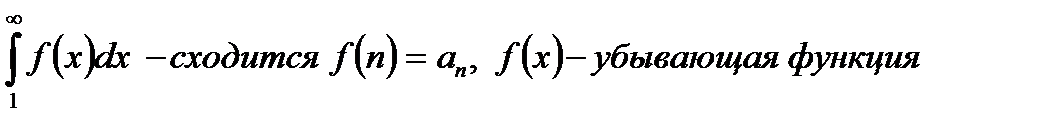 . .
|
Вопрос №35
| V1 | Достаточный признак сходимости Коши: |
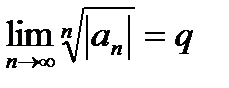 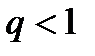 . .
| |
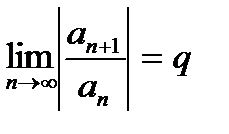 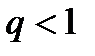 . .
| |
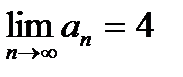
| |
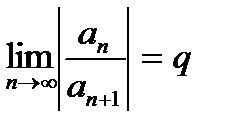 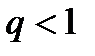 . .
| |
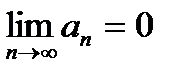 . .
| |
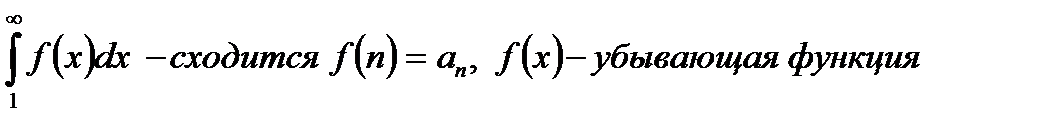 . .
|
Вопрос №36
| V1 | Необходимый признак сходимости: |
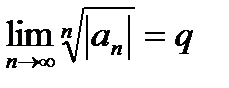 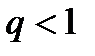 . .
| |
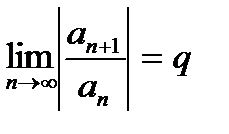 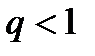 . .
| |
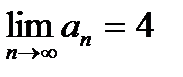
| |
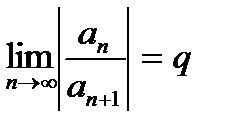 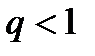 . .
| |
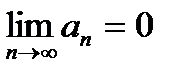 . .
| |
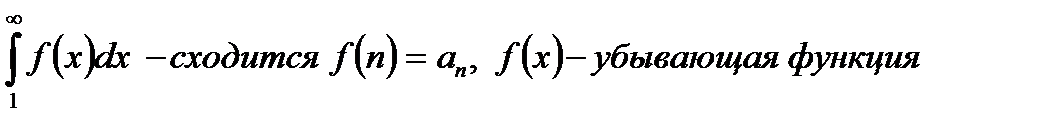 . .
|
Вопрос №37
| V1 |
На основании признака Лейбница знакочередующийся ряд 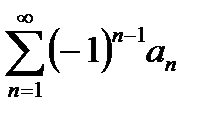 сходится, если: сходится, если:
|
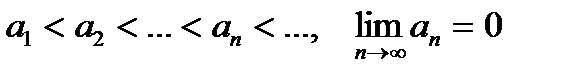
| |
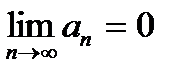
| |
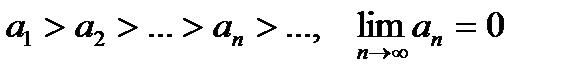
| |
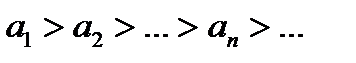
| |
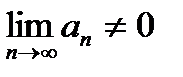
| |
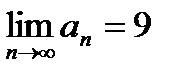
|
Вопрос №38
| V1 | Знакопеременный ряд 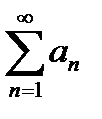 называется условно сходящимся, если: называется условно сходящимся, если:
|
ряда 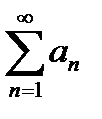 сходится, а ряд сходится, а ряд 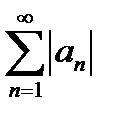 расходится. расходится.
| |
ряд 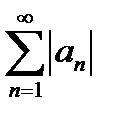 сходится. сходится.
| |
 . .
| |
| |
| |
|
Вопрос №40
| V1 | Для сходящегося ряда 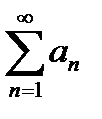 выполняется: выполняется:
|
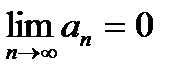
| |
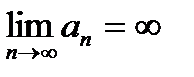
| |
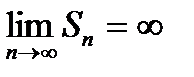
| |
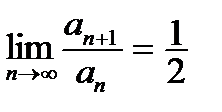
| |
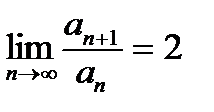
| |
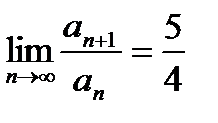
|
Вопрос №41
| V1 | Для расходящегося ряда 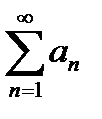 выполняется: выполняется:
|
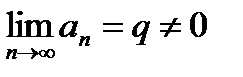
| |
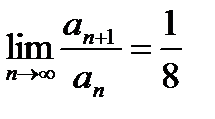
| |
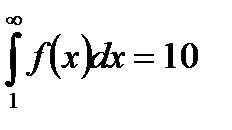
| |
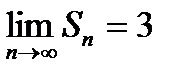
| |
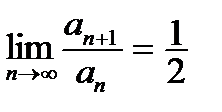
| |
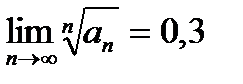
|
Вопрос №42
| V1 | Для сходящегося ряда 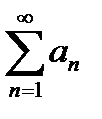 выполняется: выполняется:
|
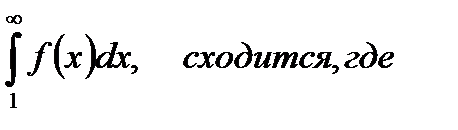 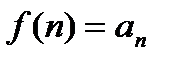
| |
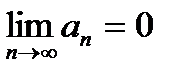
| |
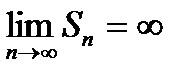
| |
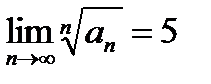
| |
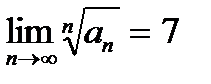
| |
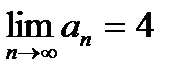
|
Вопрос №43
|
|
|
| V1 |
Для сходящегося ряда 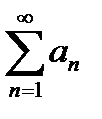 выполняется: выполняется:
|
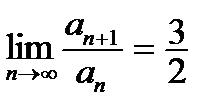
| |
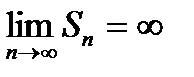
| |
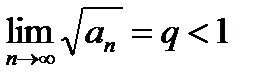
| |
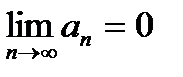
| |
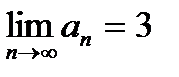
| |
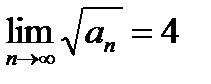
|
Вопрос №44
| V1 | Укажите абсолютно сходящийся ряд 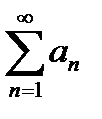 : :
|
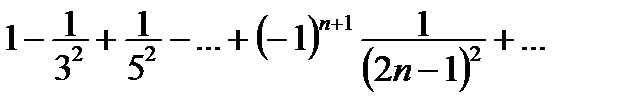
| |
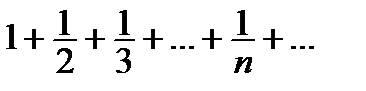
| |
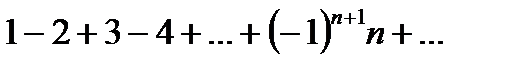
| |
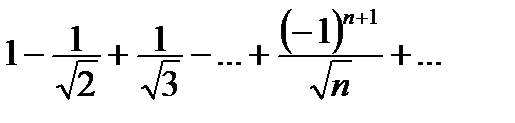
| |
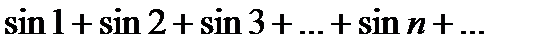
| |
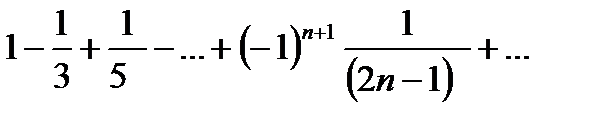
|
 2015-03-22
2015-03-22 226
226








