| V1 | Определитель 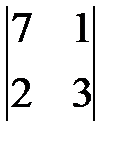 равен: равен:
|
Вопрос №4
| V1 | Алгебраическое дополнение 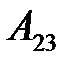 определителя определителя 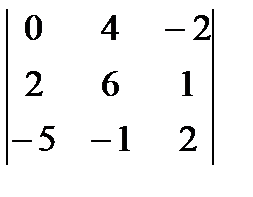 равно: равно:
|
| -34 | |
| -20 | |
Вопрос №5
| V1 | Если 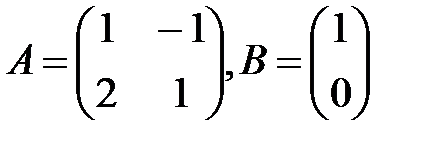 , то произведение матриц , то произведение матриц 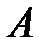 и и 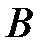 будет равно: будет равно:
|
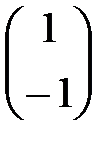
| |
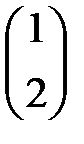
| |
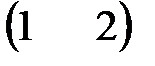 . .
| |
| (4 5) | |
| (3 4) |
Вопрос №6
| V1 | Если 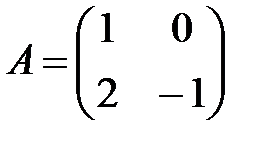 ,то обратная матрица ,то обратная матрица 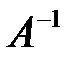 будет равна: будет равна:
|
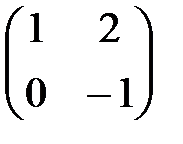
| |
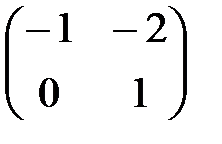
| |
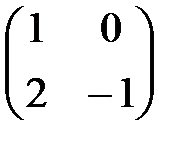
| |
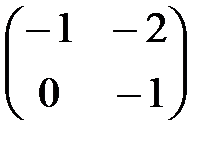
| |
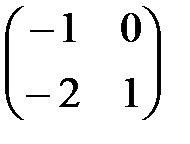
|
Вопрос №7
| V1 |
Если 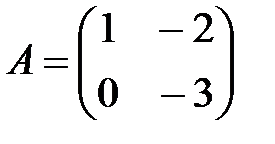 ; ; 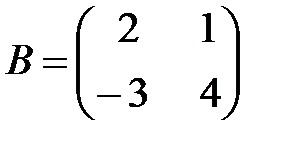 , то , то 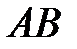 будет равно: будет равно:
|
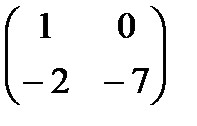
| |
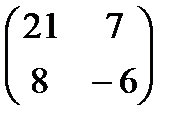
| |
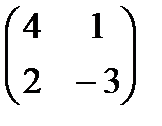
| |
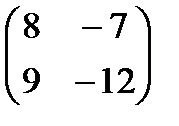
| |
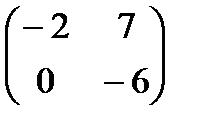
| |
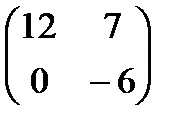
|
Вопрос №8
| V1 |
Векторы 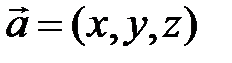 и и 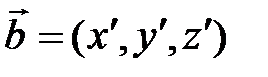 коллинеарны, если: коллинеарны, если:
|
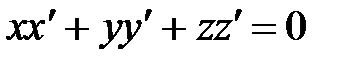
| |
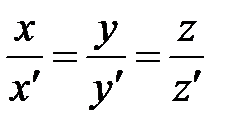
| |
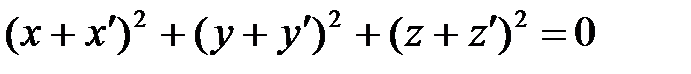
| |
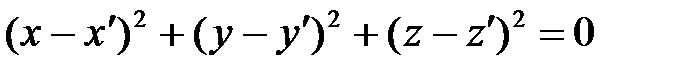
| |
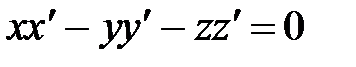
| |
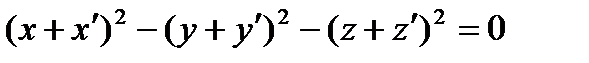
|
Вопрос №9
| V1 | Векторное произведение векторов 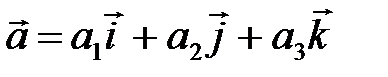 и и 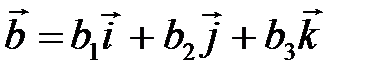 равно: равно:
|
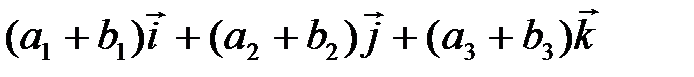
| |
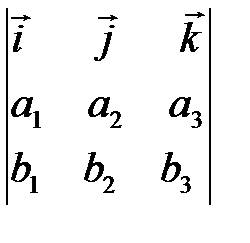
| |
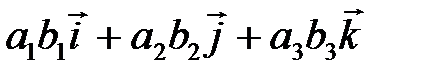
| |
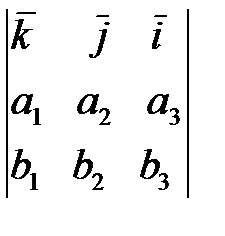
| |
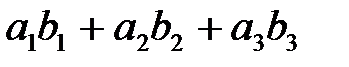
| |
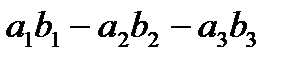
|
Вопрос №10
| V1 |
Скалярное произведение векторов 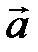 и и 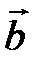 равно: равно:
|
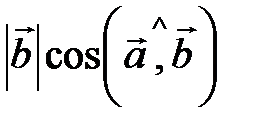
| |
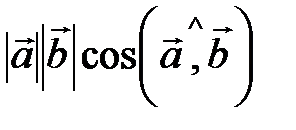
| |
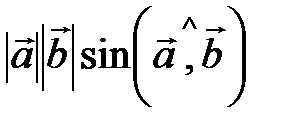
| |
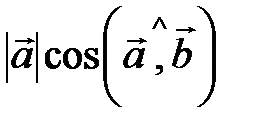
| |
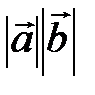
| |
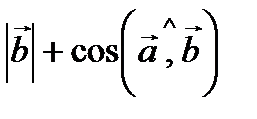
|
Вопрос 11
| V1 | Скалярное произведение векторов 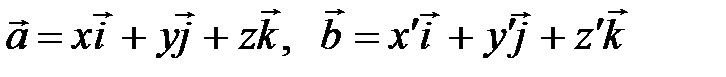 , т.е. , т.е. 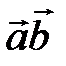 равно: равно:
|
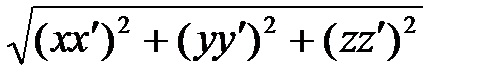
| |
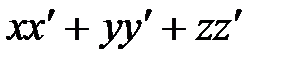
| |
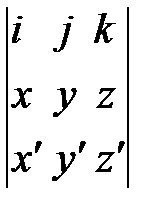
| |
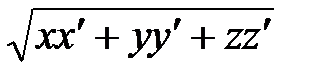
| |
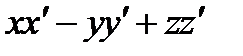
| |
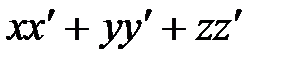
|
Вопрос №12
| V1 |
Расстояние между точками 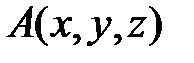 и и 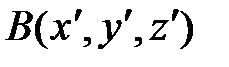 определяется формулой: определяется формулой:
|
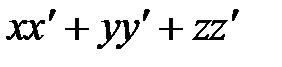 . .
| |
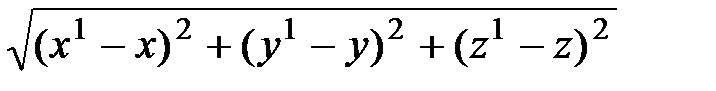
| |
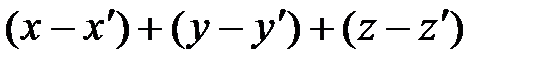
| |
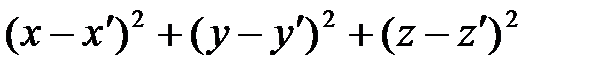
| |
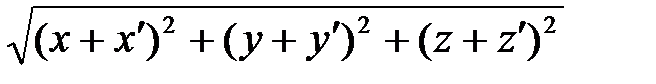
| |
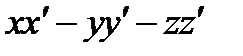
|
Вопрос №13
| V1 |
Смешанное произведение векторов 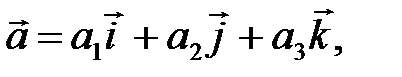 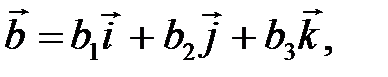 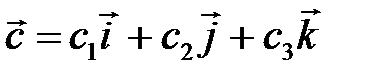 равно: равно:
|
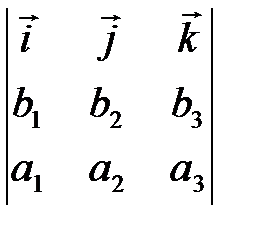
| |
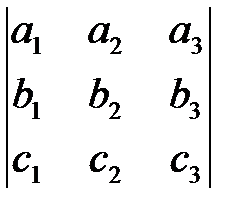
| |
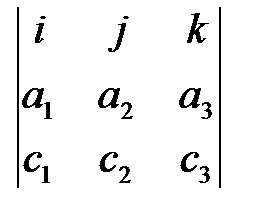
| |
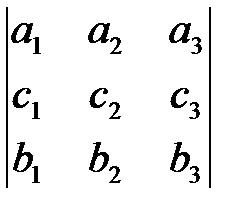
| |
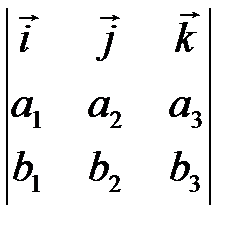
| |
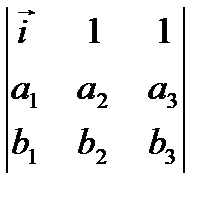
|
Вопрос №14
| V1 |
Если 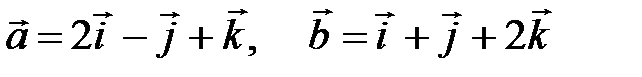 , то , то 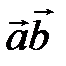 равно: равно:
|
Вопрос №15
| V1 |
Если 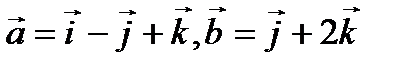 , то , то 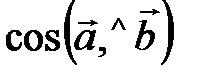 равен: равен:
|
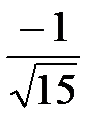
| |
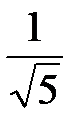
| |
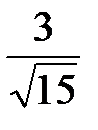
| |
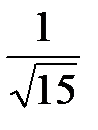
| |
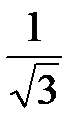
| |
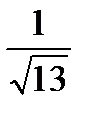
|
 2015-03-22
2015-03-22 255
255








