Найти указанные пределы:
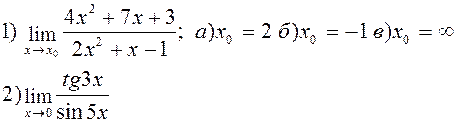
| |
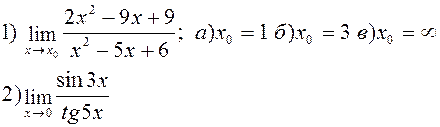
| |
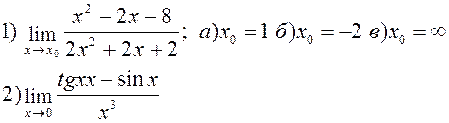
| |
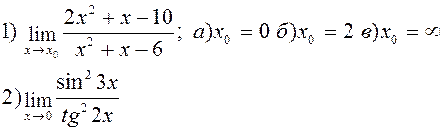
| |
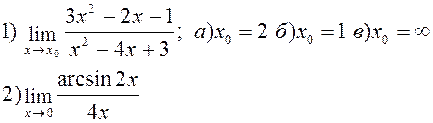
| |
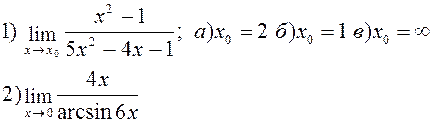
| |
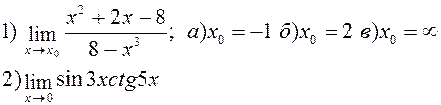
| |
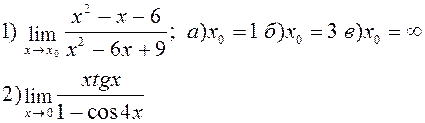
| |
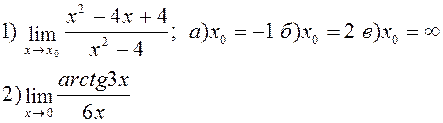
| |
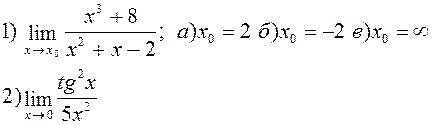
| |
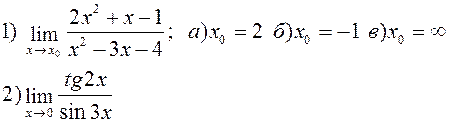
| |
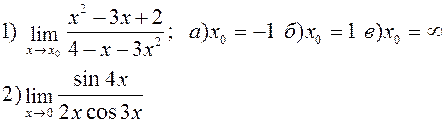
| |
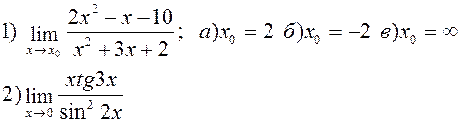
| |
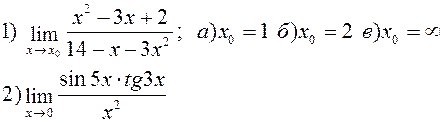
| |
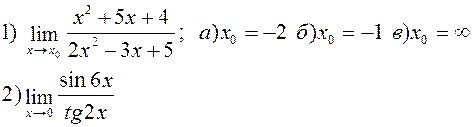
| |
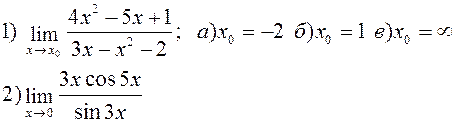
| |

| |
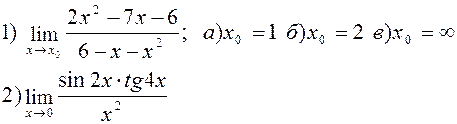
| |
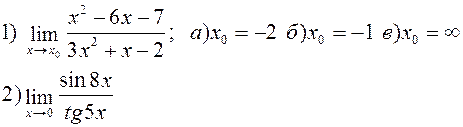
| |
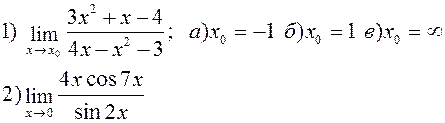
| |
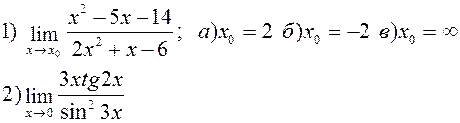
| |
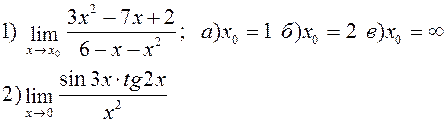
| |
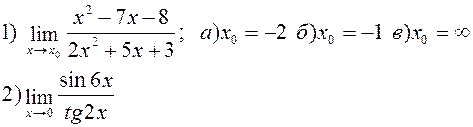
| |
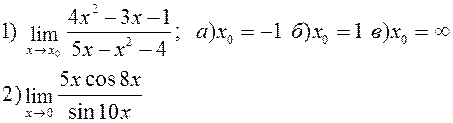
| |
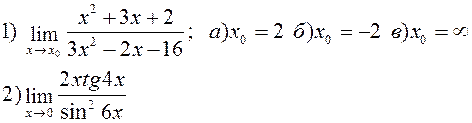
| |
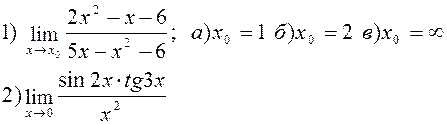
| |
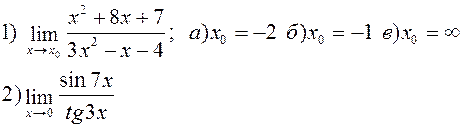
| |
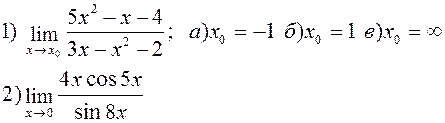
| |
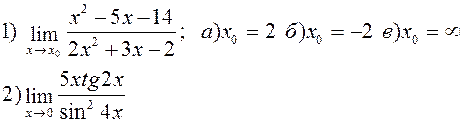
| |
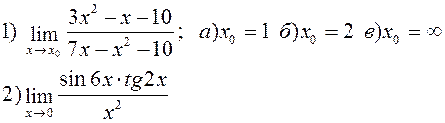
|
Задание № 2
Найти производные, пользуясь правилами и формулами дифференцирования:
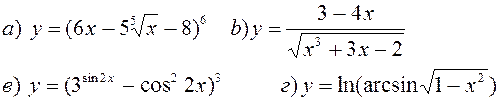
| |
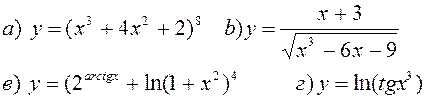
| |
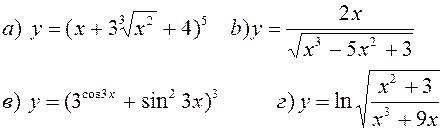
| |
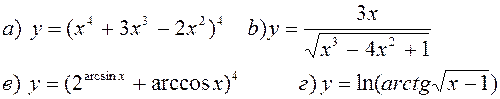
| |
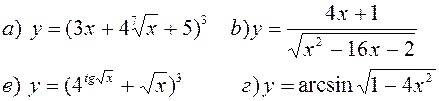
| |
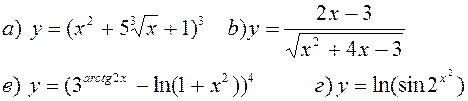
| |
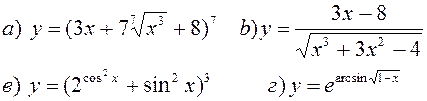
| |
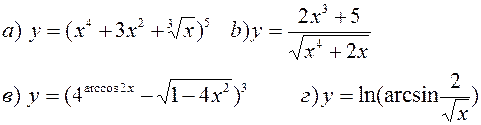
| |
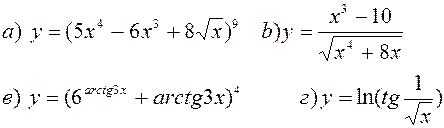
| |
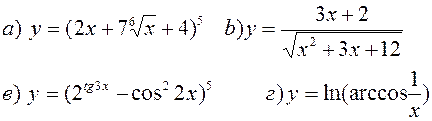
| |
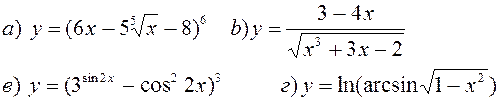
| |
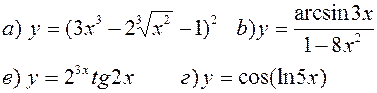
| |
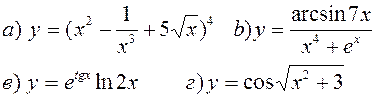
| |
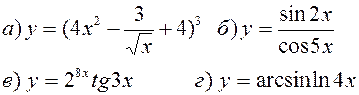
| |
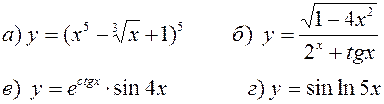
| |
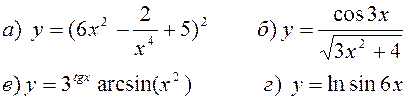
| |
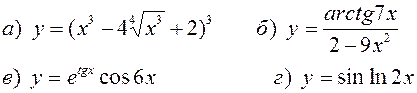
| |
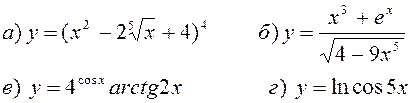
| |
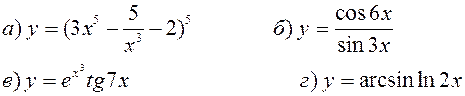
| |
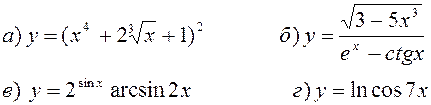
| |
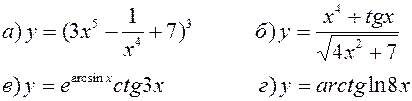
| |
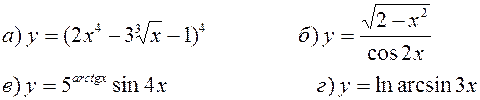
| |
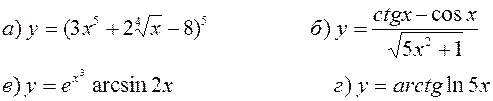
| |

| |
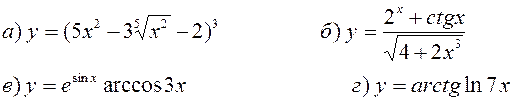
| |

| |
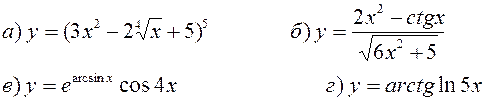
| |

| |
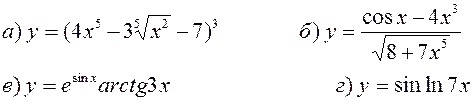
| |

|
Задание № 3
Исследовать заданные функции методами дифференциального исчисления, начертить их графики.
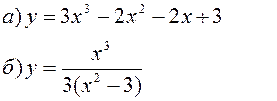
| |
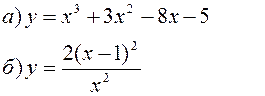
| |
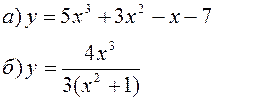
| |
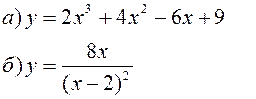
| |
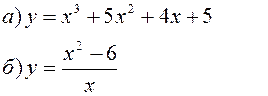
| |
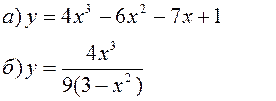
| |
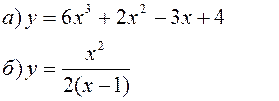
| |
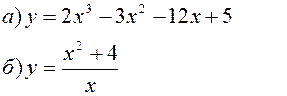
| |
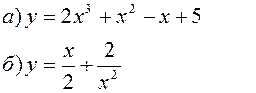
| |
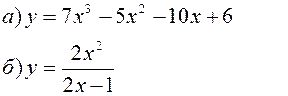
| |
 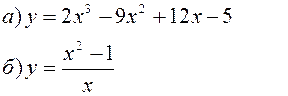
| |
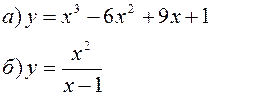
| |
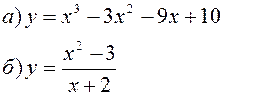
| |
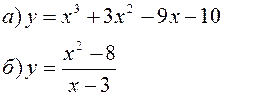
| |

| |
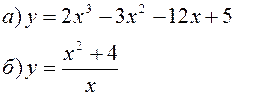
| |
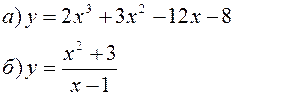
| |
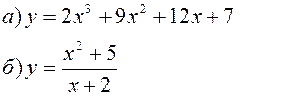
| |
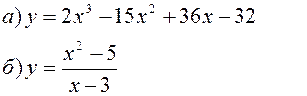
| |
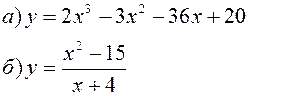
| |
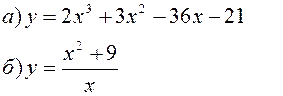
| |
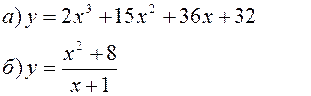
| |
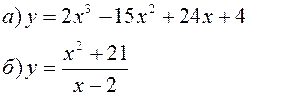
| |
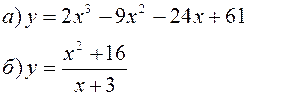
| |
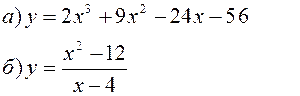
| |
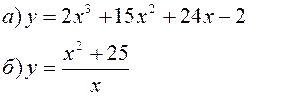
| |
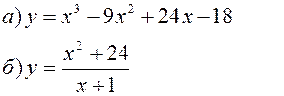
| |
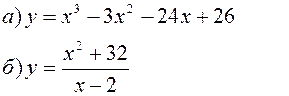
| |
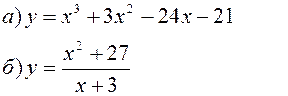
| |
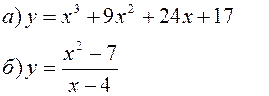
|
Решение типовых примеров для контрольной работы № 2.
Задание № 1
1. Найти неопределенный интеграл 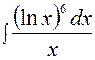
Решение. Применим подстановку 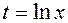 , тогда
, тогда  и
и
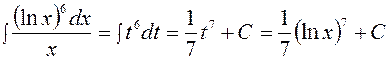 ;
;
2. Найти интеграл 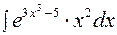 .
.
Решение. Применим подставку t =3 x 3 – 5.
Тогда 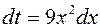 ;
; 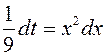 , откуда
, откуда
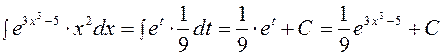 .
.
 2015-03-22
2015-03-22 582
582








