Отношения порядка и эквивалентности. Разбиения

Определение 3. Пусть X – множество. Бинарное отношение R Í X´X называется отношением порядка на X, если оно рефлексивно, антисимметри-чно и транзитивно. Таким образом, R – отношение порядка, если

(1) (a,a)ÎR для всех a Î X,

(2) aRb & bRa Þ a=b,

(3) для всех a, b, c Î X верна импликация aRb & bRc ÞaRc,

Пара (X,R), состоящая из множества X и отношения порядка R на X.

Отношение порядка обычно обозначается символом £.

Определение 4. Частично упорядоченное множество (X,£) называется нижней полурешеткой, если для любых 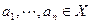множество

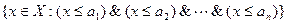
имеет наибольший элемент, который мы обозначим через Ù_1£i£n a_i. Если для любых 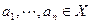множество 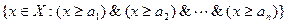имеет наименьший элемент Ú_1£i£n a_i, то оно назывется верхней полурешеткой. Если (X,£) является нижней и верхней полурешеткой, то оно называется решеткой.

Лемма 1. Если конечное частично упорядоченное множество (X,£) является нижней полурешеткой и имеет наибольший элемент, то оно является решеткой.

Доказательство. Пусть 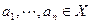. В этом случае множество

S=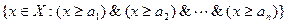

непусто и конечно. Поскольку X – нижняя полурешетка, то существует

Ù_xÎS x. Положим z= Ù_xÎS x. Для всех i=1, …, n имеет место z³ a_i. И z – наименьший среди обладающих этим свойством. Стало быть, z = Ú_1£i£n a_i.

Определение 5. Пусть X – множество. Бинарное отношение R Í X´X называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно. Таким образом, R – отношение эквивалентности на X, если

(1) (a,a)ÎR для всех a Î X,

(2) aRb Þ bRa

(3) для всех a, b, c Î X верна импликация aRb & bRc ÞaRc,

Определение 6. Разбиением множества X называется множество {X_i: iÎI} попарно непересекающихся подмножеств X_i Í X таких, что 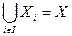. С каждым разбиением {X_i: iÎI} можно связать отношение эквивалентности ~ на X, полагая x ~ y, если x и y являются элементами некоторого X_i.

Каждому отношению эквивалентности ~ на X соответствует разбиение {X_i: iÎI}, элементами которого являются подмножества, состоящие из эквивалентных элементов. Эти подмножества называются классами эквивалентности. Разбиение {X_i: iÎI} называется фактор-множеством множества X по отношению эквивалентности ~ и обозначается: X/~.

Теорема 3. Пусть X – конечное множество. Множество отношений эквивалентности на X является решеткой относительно включения.

Доказательство. Множество отношений эквивалентности является нижней полурешеткой, ибо точной нижней гранью отношений эквивалентностей будет их пересечение. Оно будет иметь наибольший элемент X´X. Стало быть, оно будет решеткой, по лемме 1.

Замечание. Поскольку разбиения множества X взаимно однозначно соответствуют отношениям эквивалентности на X, то множество разбиений легко превратить в решетку. Отношение порядка 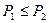между разбиениями определяется как имеющее место тогда и только тогда, когда верна импликация

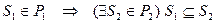
Упражнение 1. Пусть (X,R) – конечное частично упорядоченное множество. Доказать, что множество отношений порядка rÍR, упорядоченное отношением Í, будет решеткой.

Функции. Функцией или отображением 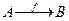называется тройка, состоящая из множеств A и B и подмножества fÍA´B (графика функции), удовлетворяющего следующим двум условиям

1. Для любого xÎA существует такой yÎf, что (x,y) Îf.

2. Если (x, y)Îf и (x, z) Îf, то y=z

Легко видеть, что fÍA´B будет тогда и только определять функцию, когда для любого xÎA существует единственный yÎf, что (x,y) Îf. Этот y обозначим через f(x).

Функция 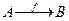называется инъекцией, если для любых x¹x’ имеет место f(x)¹f(x’). Функция 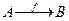называется сюръекцией, если для каждого yÎB существует такой xÎA, что f(x)=y. Если функция является инъекцией и сюръекцией, то она называется биекцией.

Теорема 4. Для того, чтобы функция 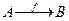была биекцией, необходимо и достаточно существования такой функции 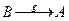, что fg=Id_B и gf=Id_A.

Пусть 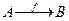- функция. Образом подмножества XÍA называется подмножество f(X) = {f(x): xÎX}Í B. Для YÍB подмножество f^-1(Y)={xÎA: f(x)ÎY} называется прообразом подмножества Y.