Отношения и функции

Перечисление элементов декартового произведения. Декартовым произведением множеств называется множество, состоящее из упорядоченных пар: A´B={(a,b): (aÎA) & (bÎB)}. Декартово произведение 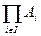семейства множеств {A_i } _i_Î_I определяется как множество, состоящее из таких функций f: I ® 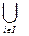A_i, что для всех iÎI верно f(i) Î A_i.

Теорема 1. A и B – конечныеÞ | A´B| = | A|×|B|.

Следствие 1. |Aⁿ|=|A|ⁿ.

Доказательство. C помощью индукции по n.

Отношения и графы.

Определение 1. Ориентированным графом называется пара множеств (E,V) вместе с парой отображений s, t: E®V. Элементы множества V изображаются точками на плоскости и называются вершинами. Элементы из E называются направленными ребрами или стрелками. Каждый элемент eÎE изображается в виде стрелки (возможно, криволинейной), соединяющей вершину s(e) с вершиной t(e).

Произвольному бинарному отношению RÍV´V соответствует ориентированный граф с вершинами vÎV, стрелками которого являются упорядоченные пары (u,v) ÎR.

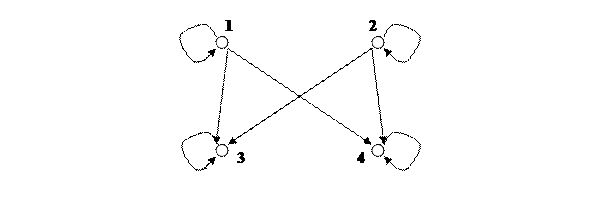
Пример 1. Пусть V={1,2,3,4}. Рассмотрим отношение R={(1,1), (1,3), (1.4), (2,2), (2,3), (2,4), (3,3), (4,4) }. Ему будет соответствовать ориентированный граф (рис. 1.1). Стрелками этого граф будут пары (i,j) ÎR.

Рис. 1.1. Ориентированный граф бинарного отношения

Определение 2. Простым (неориентированным) графом G=(V,E) называется пара, состоящая из множества V и бинарного антирефлексивного симметричного отношения EÍV´V. Элементы из V называются вершинами, а из E – ребрами.

Простой граф можно определить как множество V вершин вместе с множеством двухэлементных подмножеств EÍP(V). Вершины простого графа изображаются как точки, а ребра – как отрезки. На рис. 1.2 изображен простой граф с множеством вершин V={1, 2, 3, 4} и множеством ребер E = {{1,2}, {1,3},{1,4}, {2,3}, {2,4}, {3, 4}}.

Рис. 1.2. Простой неориентированный граф K₄

Операции над бинарными отношениями. Бинарным отношением между элементами множеств A и B называется произвольное подмножество R Í A´B. Запись aRb (при a Î A, b Î B) означает, что (a,b) Î R.

Определены следующие операции над отношениями RÍ A´A:

R^-1={(a,b): (b,a)ÎR},

R° S={(a,b): ($ xÎA)(a,x)ÎR & (x,b)ÎR},

Rⁿ=R°(Rⁿ^-1),

.

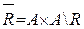Пусть Id_A = {(a,a): aÎA} – тождественное отношение. Отношение R Í X´X называется

(1) рефлексивным, если (a,a)ÎR для всех a Î X,

(2) антирефлексивным, если (a,a)ÏR для всех a Î X,

(3) симметричным, если для всех a, b Î X верна импликация aRb ÞbRa,

(4) антисимметричным, если aRb & bRa Þ a=b,

(5) транзитивным, если для всех a, b, c Î X верна импликация aRb & bRc ÞaRc,

(6) линейным, для всех a, b Î X верна импликация a¹b Þ aRb Ú bRa.

Обозначим Id_A через Id.

Теорема 2. Отношение R Í X´X

(1) рефлексивно Û Id Í R,

(2) антирефлексивно Û RÇId= Æ,

(3) симметрично Û R = R^-1,

(4) антисимметрично Û R Ç R^-1Í Id,

(5) транзитивно Û R°RÍ R

(6) линейно Û R ÈId È R^-1= X ´ X.