1. 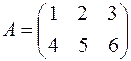 – матрица порядка
– матрица порядка 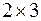 .
.
2. 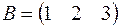 – матрица – строка порядка
– матрица – строка порядка 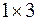 .
.
3. 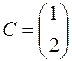 – матрица – строка порядка
– матрица – строка порядка 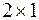 .
.
Матрица, в которой число строк совпадает с числом столбцов, называется квадратной.
Пример. 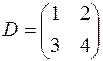 – квадратная матрица порядка
– квадратная матрица порядка 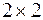 .
.
Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы, обозначаются соответствующими строчными буквами латинского алфавита с двумя правыми нижними индексами. Первый индекс обозначает номер строки, а второй – номер столбца, в которых рассматриваемый элемент матрицы находится.
Пример. 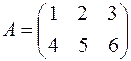 .
.
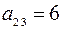 –элемент матрицы
–элемент матрицы 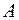 , находящийся во второй строке и в третьем столбце.
, находящийся во второй строке и в третьем столбце.
Заметим, что матрицу 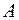 порядка
порядка 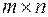 можно записать так:
можно записать так:
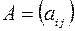 ,
, 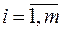 ;
; 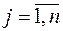 .
.
Две матрицы порядка 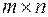 считаются равными, если все соответствующие элементы этих матриц равны. То есть
считаются равными, если все соответствующие элементы этих матриц равны. То есть 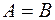 , если
, если 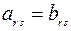 для любых возможных
для любых возможных 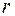 и
и 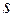 .
.
Пример. 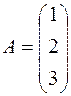 ,
, 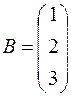 . Матрицы
. Матрицы 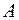 и
и 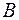 равны, так как
равны, так как 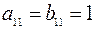 ,
, 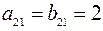 ,
, 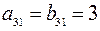 .
.
Произведением матрицы 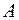 порядка
порядка 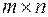 на действительное число
на действительное число 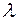 называется матрица
называется матрица 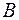 того же порядка
того же порядка 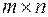 , каждый элемент
, каждый элемент 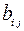 ,
, 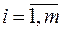 ,
, 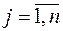 которой получен умножением соответствующего элемента
которой получен умножением соответствующего элемента 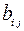 ,
, 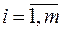 ,
, 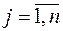 исходной матрицы
исходной матрицы 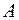 на число
на число 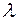 и обозначается:
и обозначается: 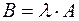 .
.
Пример. Найти 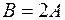 , если
, если 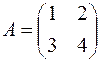 .
.
Решение. 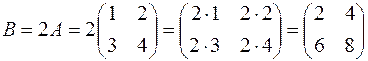 .
.
Ответ: 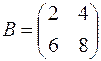 .
.
Суммой двух матриц 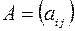 и
и 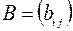 одного порядка
одного порядка 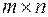 называется матрица
называется матрица 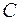 того же порядка
того же порядка 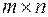 , каждый элемент
, каждый элемент 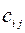 ,
, 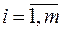 ,
, 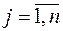 которой получен сложением соответствующих элементов
которой получен сложением соответствующих элементов 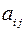 и
и 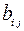 ,
, 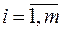 ,
, 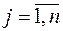 и обозначается
и обозначается 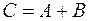 .
.
Пример. Найти 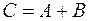 , если
, если 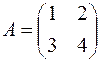 и
и 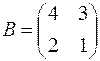 .
.
Решение. 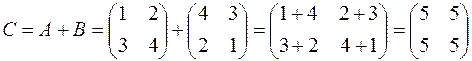 .
.
Ответ: 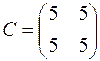 .
.
Заметим, что разность двух матриц 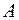 и
и 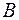 одного и того же порядка можно определить через сумму и умножение на число
одного и того же порядка можно определить через сумму и умножение на число 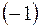 , то есть
, то есть 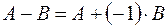 .
.
Пример. Найти 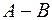 , если
, если 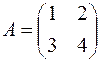 и
и 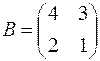 .
.
Решение. 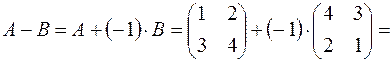
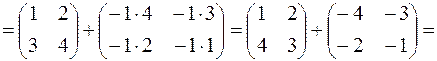
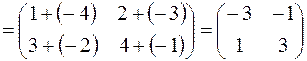 .
.
Ответ: 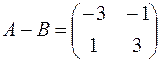 .
.
Произведением матрицы 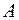 порядка
порядка 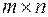 на матрицу
на матрицу 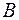 порядка
порядка 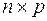 называется матрица
называется матрица 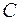 порядка
порядка 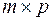 , каждый элемент
, каждый элемент 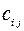 ,
, 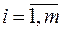 ,
, 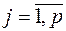 которой получен как произведение элементов
которой получен как произведение элементов 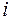 -ой строки матрицы
-ой строки матрицы 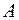 на соответствующие элементы
на соответствующие элементы 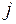 -го столбца матрицы
-го столбца матрицы 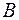 , то есть
, то есть 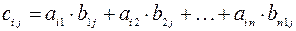 ,
, 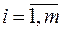 ,
, 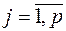 и обозначается:
и обозначается: 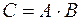 .
.
Пример. Найти 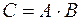 , если
, если 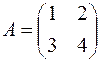 и
и 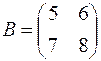 .
.
 2015-03-22
2015-03-22 452
452








