Системы линейных уравнений

Пусть задана система трех линейных алгебраических уравнений с тремя неизвестными вида:

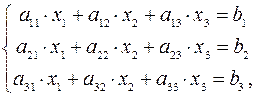(1.1)

где , , .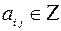

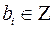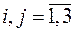Составим и вычислим главный определитель системы (1.1):

,

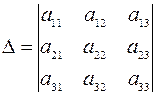тогда если 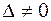, то система (1.1) имеет единственное решение 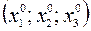, которое находим по правилу Крамера. Для этого, составим и вычислим вспомогательные определители 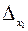, , 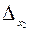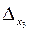системы (1.1):

, , .

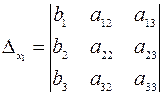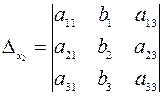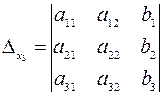Далее, по формулам Крамера, находим:

, , .

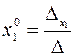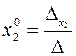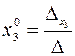Затем делаем проверку найденного решения и записываем ответ.

Пример. Решить по правилу Крамера систему .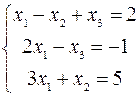

Решение. Составим и вычислим главный определитель данной системы:

.

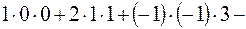
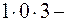
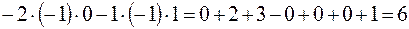Так как 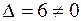, то данная система имеет единственное решение.

Составим и вычислим вспомогательные определители данной системы:

;

;

.

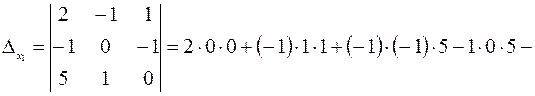
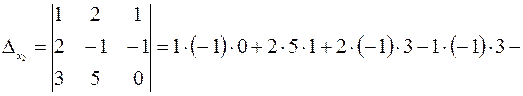
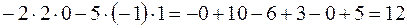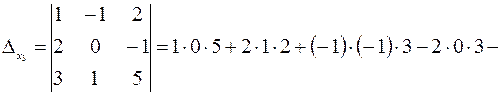
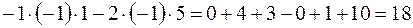Далее, по формулам Крамера, находим:

, , .

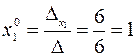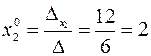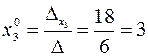Делаем проверку найденного решения :

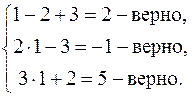
Ответ: .