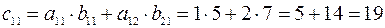
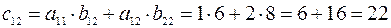
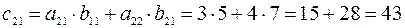
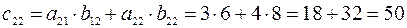 .
.
Следовательно, 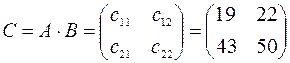 .
.
Ответ: 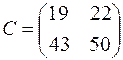 .
.
Следует обратить внимание на тот факт, что:
1) произведение 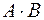 матриц
матриц 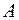 и
и 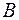 получается умножением элементов строк матрицы
получается умножением элементов строк матрицы 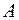 – первого сомножителя – на элементы столбцов матрицы
– первого сомножителя – на элементы столбцов матрицы 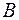 – второго сомножителя. Следовательно, порядок сомножителей в произведении матриц важен;
– второго сомножителя. Следовательно, порядок сомножителей в произведении матриц важен;
2) число столбцов матрицы 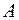 должно быть равно числу строк матрицы
должно быть равно числу строк матрицы 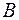 , в противном случае произведение матриц
, в противном случае произведение матриц 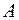 и
и 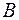 не определено;
не определено;
3) порядок матрицы-произведения определяется порядком сомножи-телей, то есть 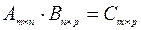 . Следовательно, если
. Следовательно, если 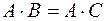 , то нельзя считать, что
, то нельзя считать, что 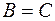 .
.
Транспонированной матрицей (обозначаемой как  ) любой матрицы
) любой матрицы 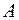 порядка
порядка 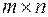 называется матрица
называется матрица  порядка
порядка 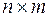 , которая получается из матрицы
, которая получается из матрицы 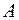 взаимной заменой строк на столбцы.
взаимной заменой строк на столбцы.
Пример. Найти  , если
, если 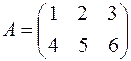 .
.
Решение. Элементы первой строки матрицы 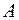 запишем в первый столбец матрицы
запишем в первый столбец матрицы  , а элементы второй строки матрицы
, а элементы второй строки матрицы 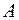 – во второй столбец матрицы
– во второй столбец матрицы  , получаем:
, получаем: 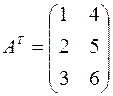 .
.
 2015-03-22
2015-03-22 425
425








