2015-03-22
804
Необходимо сделать еще одно замечание: числа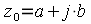 
и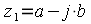 
называются комплексно-сопряженными. При этом комплексно-сопряженное число обозначается чертой 
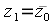Согласно выражениям (3) и (7) их модули равны, а фазы равны по модулю но имеют противоположные знаки:
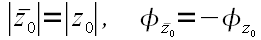 . | (21) |
Произведение согласно выражению (19) равно:
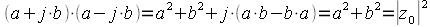 . | (22) |
Таким образом произведение комплексно-сопряженных чисел есть действительное число равное квадрату модуля этих чисел. Векторное представление комплексно-сопряженных чисел представлено на рисунке 6.
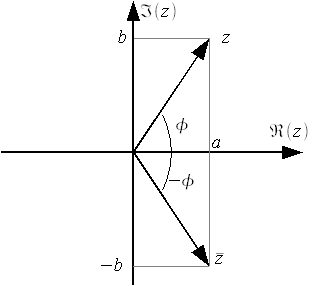
Рисунок 6: Векторное представление комплексно-сопряженных чисел
