Уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818).
Нормальное уравнение ввёл Л. О. Гессе (1861).
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть заданауравнением первой степени.
- Общее уравнение (полное) плоскости
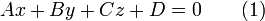
где 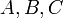 и
и 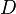 — постоянные, причём
— постоянные, причём 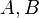 и
и 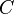 одновременно не равны нулю; в векторной форме:
одновременно не равны нулю; в векторной форме:
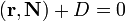
где 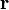 — радиус-вектор точки
— радиус-вектор точки 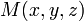 , вектор
, вектор 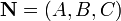 перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора
перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора 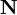 :
:
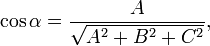
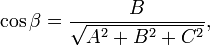
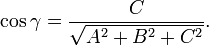
Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При 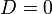 плоскость проходит через начало координат, при
плоскость проходит через начало координат, при 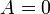 (или
(или 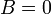 ,
, 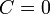 ) П. параллельна оси
) П. параллельна оси 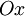 (соответственно
(соответственно 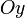 или
или 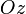 ). При
). При 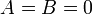 (
(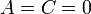 , или
, или 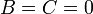 ) плоскость параллельна плоскости
) плоскость параллельна плоскости 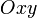 (соответственно
(соответственно 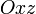 или
или 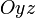 ).
).
- Уравнение плоскости в отрезках:

где 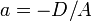 ,
, 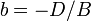 ,
, 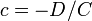 — отрезки, отсекаемые плоскостью на осях
— отрезки, отсекаемые плоскостью на осях 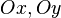 и
и 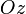 .
.
- Уравнение плоскости, проходящей через точку
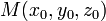 перпендикулярно вектору нормали
перпендикулярно вектору нормали 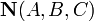 :
:
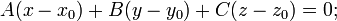
в векторной форме:
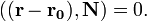
- Уравнение плоскости, проходящей через три заданные точки
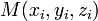 , не лежащие на одной прямой:
, не лежащие на одной прямой:
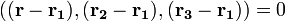
(смешанное произведение векторов), иначе
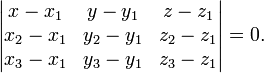
- Нормальное (нормированное) уравнение плоскости
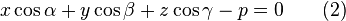
в векторной форме:
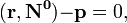
где 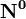 - единичный вектор,
- единичный вектор, 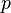 — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
— расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
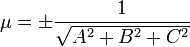
(знаки  и
и 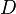 противоположны).
противоположны).
Определение по точке и вектору нормали[править | править вики-текст]
В трехмерном пространстве одним из важнейших способов определения плоскости является указание точки на плоскости и вектора нормали к ней.
Допустим, 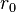 является радиусом-вектором точки
является радиусом-вектором точки 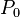 , заданной на плоскости, и допустим, что n - это ненулевой вектор, перпендикулярный к плоскости (нормаль). Идея состоит в том, что точка
, заданной на плоскости, и допустим, что n - это ненулевой вектор, перпендикулярный к плоскости (нормаль). Идея состоит в том, что точка 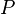 с радиусом-вектором r находится на плоскости тогда и только тогда, когда вектор, проведённый от
с радиусом-вектором r находится на плоскости тогда и только тогда, когда вектор, проведённый от 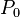 к
к 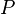 , перпендикулярен n.
, перпендикулярен n.
Вернёмся к тому, что два вектора являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю. Отсюда следует, что нужная нам плоскость может быть выражена как множество всех точек r таких, что:
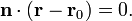 (Здесь точка означает скалярное произведение, а не умножение.)
(Здесь точка означает скалярное произведение, а не умножение.)
Развернув выражение, мы получим:
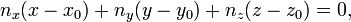
что является знакомым нам уравнением плоскости.
Например: Дано: точка на плоскости 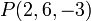 и вектор нормали
и вектор нормали 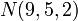 .
.
Уравнение плоскости записывается так:
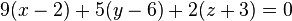
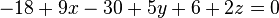
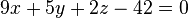
24. Уравнения прямых в трехмерном точечном евклидовом пространстве.
Векторное параметрическое уравнение прямой в пространстве:
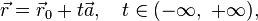
где 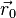 — радиус-вектор некоторой фиксированной точки
— радиус-вектор некоторой фиксированной точки 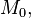 лежащей на прямой,
лежащей на прямой, 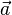 — ненулевой вектор, коллинеарный этой прямой (называемый её направляющим вектором),
— ненулевой вектор, коллинеарный этой прямой (называемый её направляющим вектором), 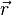 — радиус-вектор произвольной точки прямой.
— радиус-вектор произвольной точки прямой.
Параметрические уравнения прямой в пространстве:
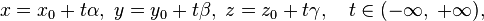
где 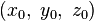 — координаты некоторой фиксированной точки
— координаты некоторой фиксированной точки 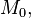 лежащей на прямой;
лежащей на прямой; 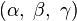 — координаты вектора, коллинеарного этой прямой.
— координаты вектора, коллинеарного этой прямой.
Каноническое уравнение прямой в пространстве:
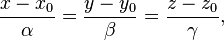
где 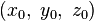 — координаты некоторой фиксированной точки
— координаты некоторой фиксированной точки 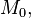 лежащей на прямой;
лежащей на прямой; 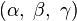 — координаты вектора, коллинеарного этой прямой.
— координаты вектора, коллинеарного этой прямой.
Общее векторное уравнение прямой [ уточнить ] в пространстве:
Поскольку прямая является пересечением двух различных плоскостей, заданных соответственно общими уравнениями:
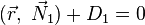 и
и 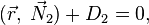
то уравнение прямой можно задать системой этих уравнений:
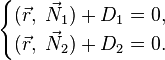
Векторное уравнение прямой в пространстве [1]:196-199:
Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой 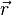 на фиксированный направляющий вектор прямой
на фиксированный направляющий вектор прямой 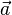 :
:
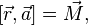
где фиксированный вектор 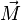 , ортогональный вектору
, ортогональный вектору 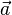 , можно найти, подставляя в это уравнение радиус-вектор какой-нибудь одной известной точки прямой.
, можно найти, подставляя в это уравнение радиус-вектор какой-нибудь одной известной точки прямой.
25. Взаимное расположение прямых и плоскостей, расстояние между ними.
26. Кривые второго порядка, их канонические уравнения в прямоугольной декартовой системе координат. Приведение кривых второго порядка к каноническому виду.
Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида
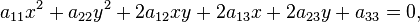
в котором по крайней мере один из коэффициентов 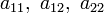 отличен от нуля.
отличен от нуля.
Вид кривой зависит от четырёх инвариантов:
инварианты относительно поворота и сдвига системы координат:

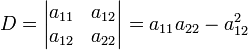
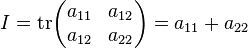
инвариант относительно поворота системы координат (полуинвариант):[ источник не указан 529 дней ]
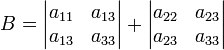
27. Поверхности второго порядка, их классификация и простейшие свойства.
Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида
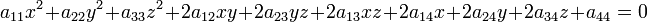
в котором по крайней мере один из коэффициентов 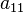 ,
, 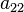 ,
, 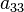 ,
, 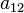 ,
, 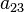 ,
, 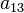 отличен от нуля.
отличен от нуля.
Цилиндрические поверхности[править | править вики-текст]
Поверхность 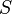 называется цилиндрической поверхностью с образующей
называется цилиндрической поверхностью с образующей 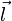 , если для любой точки
, если для любой точки 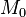 этой поверхности прямая, проходящая через эту точку параллельно образующей
этой поверхности прямая, проходящая через эту точку параллельно образующей 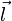 , целиком принадлежит поверхности
, целиком принадлежит поверхности 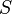 .
.
Теорема (об уравнении цилиндрической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность 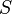 имеет уравнение
имеет уравнение 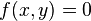 , то
, то 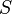 — цилиндрическая поверхность с образующей, параллельной оси
— цилиндрическая поверхность с образующей, параллельной оси 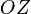 .
.
Кривая, задаваемая уравнением 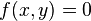 в плоскости
в плоскости 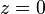 , называется направляющей цилиндрической поверхности.
, называется направляющей цилиндрической поверхности.
Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.
28. Понятия окрестностей вещественного числа. Пределы числовых последовательностей, их свойства.
29. Принцип Коши. Теорема существования пределов монотонных ограниченных последовательностей.
30. Пределы вещественных функций одной вещественной переменной и её геометрический смысл.
31. Первый замечательный предел
 2015-03-22
2015-03-22 510
510








