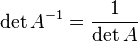Свойства обратной матрицы

, где 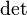обозначает определитель.

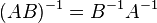для любых двух обратимых матриц 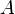и .

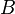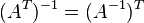, где 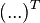обозначает транспонированную матрицу.

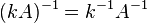для любого коэффициента .

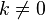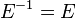Если необходимо решить систему линейных уравнений 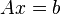, (b — ненулевой вектор) где 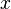— искомый вектор, и если 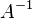существует, то 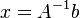. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

13. Системы линейных алгебраических уравнений, содержащие n неизвестных и n уравнений. Условие разрешимости таких систем. Матричный метод их решения, формулы Крамера.

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

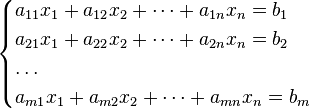
Здесь 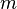— количество уравнений, а 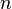— количество неизвестных. x ₁, x ₂, …, x_n — неизвестные, которые надо определить. a ₁₁, a ₁₂, …, a_mn — коэффициенты системы — и b ₁, b ₂, … b_m — свободные члены — предполагаются известными^[1]. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[2].

Система (1) называется однородной, если все её свободные члены равны нулю (b ₁ = b ₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c ₁, c ₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c ₁⁽¹⁾, c ₂⁽¹⁾, …, c_n ⁽¹⁾ и c ₁⁽²⁾, c ₂⁽²⁾, …, c_n ⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

14. Линейные (векторные) пространства. Линейные зависимые и независимые системы векторов, Базис линейного пространства. Теорема об инвариантности размерности конечномерного пространства.

Векторное (линейное) пространство — это математическая структура, которая формируется набором элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр^[1]. Введённые операции подчинены восьми аксиомам.^[^⇨^] Скаляром же может являться элементвещественного, комплексного или любого другого поля чисел. Частным случаем векторов подобного пространства являются обычные евклидовы вектора, которые используются, к примеру, для демонстрации физических сил. При этом следует отметить, что вектор как элемент векторного пространства не обязательно должен быть представлен в качестве направленного отрезка. Обобщение понятия «вектор» до элемента векторного пространства любой природы не только не вызывает смешения терминов, но и позволяет уяснить или даже предвидеть ряд результатов, справедливых для пространств произвольной природы^[2].

Линейное, или векторное пространство 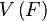над полем 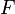— это упорядоченная четвёрка 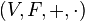, где

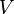— непустое множество элементов произвольной природы, которые называются векторами;

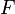— (алгебраическое) поле, элементы которого называются скалярами;

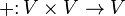— операция сложения векторов, сопоставляющая каждой паре элементов 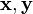множества 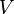единственный элемент множества 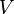, обозначаемый ;

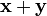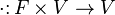— операция умножения векторов на скаляры, сопоставляющая каждому элементу 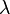поля 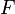и каждому элементу 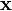множества 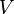единственный элемент множества 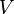, обозначаемый ;

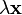причём, заданные операции удовлетворяют следующим аксиомам — аксиомам линейного (векторного) пространства:

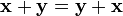, для любых 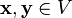(коммутативность сложения);

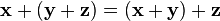, для любых 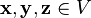(ассоциативность сложения);

существует такой элемент 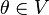, что 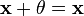для любого 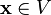(существование нейтрального элемента относительно сложения), в частности 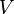не пусто;

для любого 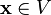существует такой элемент 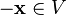, что 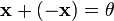(существование противоположного элемента относительно сложения).

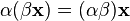(ассоциативность умножения на скаляр);

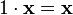(унитарность: умножение на нейтральный (по умножению) элемент поля F сохраняет вектор).

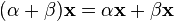(дистрибутивность умножения на вектор относительно сложения скаляров);

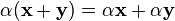(дистрибутивность умножения на скаляр относительно сложения векторов).

Таким образом, операция сложения задаёт на множестве 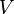структуру (аддитивной) абелевой группы.

15. Законы преобразования координат векторов при изменении базиса.

Пусть системы векторов e = {e ₁,..., e _n } и f = {f ₁,..., f _n } — два базиса n -мерного линейного пространства L_n.

Обозначим x_e = (x ₁, x ₂,..., x _n) и x_f = (x' ₁, x' ₂,..., x' _n) — координаты вектора x ∈ L_n соответственно в базисах e и f.

Справедливо следующее x_e = C _e→f ·x _f:

Здесь C _e→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f₁,..., f _n в базисе e ₁,..., e _n:

f₁ = с ₁₁· e₂ + с ₂₁ ·e₁+... + с _n ₁ ·e _n, f₂ = с ₁₂· e₁ + с ₂₂ ·e₂+... + с _n ₂ ·e _n, ..., f _n = с _{1 n}· e₂ +... + с _nn ·e _n.

Формулу преобразования координат вектора при изменении базиса принято записывать в виде

x_f = (C _e→f)^{− 1} ·x _e

16. Евклидово пространство. Неравенство Каши- Буняковского. Ортогональный и ортонормированный базис. Понятие об унитарном пространстве.

Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность равную 3.

В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов: конечномерное вещественное векторное пространство 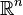с введённым на нём положительно определённым скалярным произведением, либо метрическое пространство, соответствующее такому векторному пространству. В этой статье за исходное будет взято первое определение.

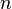-мерное евклидово пространство обозначается 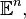также часто используется обозначение 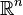(если из контекста ясно, что пространство обладает евклидовой структурой).

17. Линейные операторы. Закон преобразования матрицы линейного оператора при изменении базиса. Понятие о тензорах.

Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из X в Y.

Действие оператора обозначают y = A (x), y — образ x, x — прообраз y.

Если каждый элемнт y из Y имеет единственный прообраз x из X, y = A (x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора.

Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов u и v из X и любого числа α справедливо: