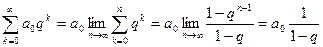Пример 1. Вычислим производящие функции некоторых последова-тельностей. С этой целью сначала вспомним формулу для суммы бесконечной геометрической прогрессии

.

С помощью этой формулы найдем производящую функцию для последовательности a_n=1, которая будет равна 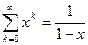. Почленное дифференцирование полученного равенства

1 + x + x² + × × × + xⁿ + × × × = .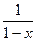

приводит к производящей функции для последовательности a_n=n+1:

1 + 2x + 3x² + × × × +(n+1)xⁿ + × × × = .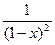

Почленное интегрирование приводит к производящей функции последовательности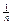

x + 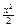+ × × × + 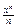+ × × × = 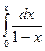= -ln(1-x)

Имеют место следующие свойства производящих функций:

1) Сумме последовательностей соответствует сумма производящих функций;

2) Производящая функция последовательности

c_n = a₀ b_n + a₁ b_n-1 + × × × + a_n b₀

равна произведению производящих функций последовательностей {a_n } и {b_n}.