2015-03-07
206
Вычислим производящую функцию F(x) чисел Фибоначчи F0 = F1 = 1, Fn+1 = Fn + Fn-1 при n ³ 1. Имеют место соотношения:
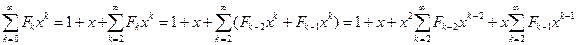
Приходим к уравнению F(x)=1 + x + x2 + x(F(x)-1) для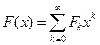 
. Решая это уравнение, получаем 
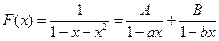, для некоторых A, B, при 
, 
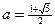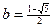. Отсюда мы видим, что ряд F(x) равен сумме геометрических прогрессий. Находим 
, 
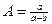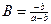. Следовательно, 
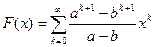. Отсюда получаем формулу для вычисления k –го числа Фибоначчи, 
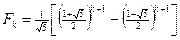, для всех k = 0, 1, 2, ∙ ∙ ∙.
