Вопрос Интегрирование иррациональных функций. Интегрирование тригонометрических функций

Для интегрирования иррациональной функции, содержащей 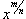используется подстановка .

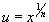Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней x, применяется подстановка в форме 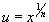, где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию.

Рациональная функция x под знаком корня n -ой степени, т.е. выражение вида 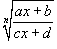, интегрируется с помощью подстановки .

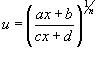Найти интеграл .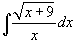

Решение.

Сделаем подстановку:

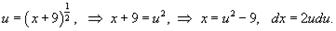
Вычислим интеграл

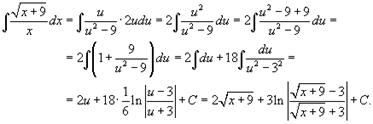
Вопрос Определенный интеграл. Его геометрический смысл и основные свойства.

Вопрос Дифференцирование интеграла по верхнему пределу. Формула Ньютона – Лейбница. Замена переменной и интегрирование по частям в определенном интеграле.