Пусть функция f (x) непрерывна при любом x ≥ a и F (x) – её первообразная. Тогда
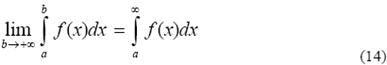
называют несобственным интегралом на бесконечном интервале. Если предел конечный, то интеграл называют сходящимся, а если предел равен бесконечности или не существует – расходящимся.
Аналогично определяются несобственный интеграл с бесконечным нижним пределом
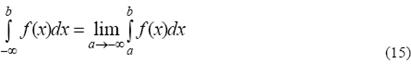
и несобственный интеграл с обоими бесконечными пределами
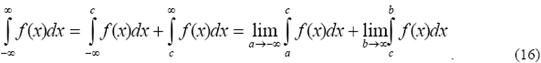
В последнем случае, если оба предела конечны, то интеграл называется сходящимся. Если F (x) – первообразная для функции f (x), то
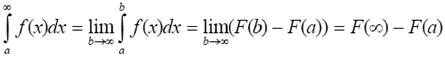
П р и м е р. Вычислить несобственные интегралы или установить их расходимость:
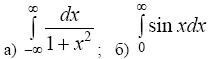
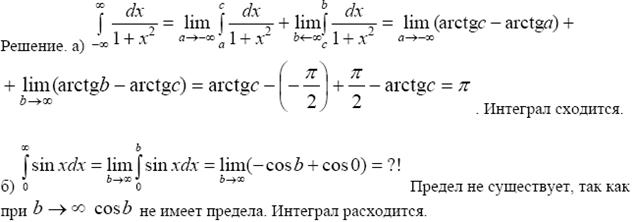
 2015-03-22
2015-03-22 1099
1099








