Решение

1) 1011 2) 1011 3) 1011

* * *

0001 0001 0011

____ ____ ____

0001011 0010110 1011

_____

4) 1011 5) 1011 6) 1011 7) 1011

* * * *

0100 0101 0110 0111

____ ____ ____ ____

01011100 1011 10110 1011

1011 1011 1011

______ _______ 1011

0100111 0111010 ______

8) 1011 9) 1011 10) 1011 11) 1011

* * * *

1000 1001 1010 1011

____ ____ _____ _____

1011000 1011 1011 1011

1011 1011 1011

_______ _________ 1011

1010011 1001110 ________

12) 1011 13) 1011 14) 1011 15) 1011

* * * *

1100 1101 1110 1111

_____ _____ ____ _____

1011 1011 1011 1011

1011 1011 1011 1011

_________ 1011 1011 1011

1110100 _________ ________ 1011

1111111 1100010 _________

Сгруппировав 14 ив 15 полученных комбинаций в колонки I и II, легко проследить циклический сдвиг одной комбинации по отношению к другой:

1) 0011101 8) 0001011 15) 1111111

2) 0111010 9) 0010110

3) 1110100 10) 0101100

4) 1101001 11) 1011000

5) 1010011 12) 0110001

б) 0100111 13) 1100010

7) 1001110 14) 1000101

Задача 6 104. Использовав метод, примененный в предыдущей задаче, построить циклический код на 14 кодовыхкомбинаций, применяя для построения образующий многочлен x³+ х²+1. Сравнить полученный код с кодом, построенным в предыдущей задаче.

Задача 6.105. Можно ли использовать неприводимый многочлен x⁵+х²+1 в качестве образующего для построения циклического кода с минимальным кодовым расстоянием d₀ = 5?

Задача 6.106. Выбрать рациональное число строк единичной матрицы для построения циклического кода, если в качестве обра- зующего многочлена используется неприводимый многочлен вида х⁵ + х⁴+ х³ + х+ 1; другим условием является возможность передачи минимум 10' сообщений и, наконец, код должен исправлять минимум одну ошибку.

Р е ш е н и е. Порядок многочлена равен 5, число ненулевых членов образующего многочлена равно 5, значит код, с одной стороны, обеспечивает кодовое расстояние между кодовыми словами, равное d₀ = 5, с другой стороны, число контрольных разрядов также равно 5. Используя табл. 3 приложения 9, выбираем максимально возможное количество информационных разрядов n_и = 26. Следовательно, число строк единичной матрицы равно 26. Первая строка образующей матрицы имеет вид:

0000000000000000000000000111011.

Код, исправляющий 2 ошибки, нельзя строить, так как не будет соблюдено второе условие; максимальное число информационных разрядов кода, исправляющего 2 ошибки, согласно табл. 2 прило- жения 9, равно 2 при n_к= 5.

Задача 6.107. Какое максимальное число ошибок может быть исправлено кодом, построенным при помощи образующего много- члена вида х⁴ + х + 1?

Задача 6.108. Используя метод образующих матриц, построить циклический код, исправляющий одиночные ошибки при передаче комбинаций четырехзначного двоичного кода на всесочетания (кроме нулевой комбинации).

Р е ш е н и е. 1) Код, обнаруживающий двойные или исправляющий одиночные ошибки, должен обеспечивать между комбинациями кодовое расстояние d₀ = 3, следовательно, число разрядов дополни- тельной матрицы n_к = 3, а каждый остаток содержит три разряда.

2) Из табл. 1 приложения 9 выбираем многочлен, степень которого больше или равна 3, число ненулевых членов также должно быть больше или равно 3. Выбранный многочлен – х³+ х²+ 1.

3) Число строк (столбцов) транспонированной матрицы n_и = 4, так как исходный код четырехразрядный.

4) Число единиц в каждом остатке (вес остатка), полученном от деления единицы с нулями на образующий многочлен, должно быть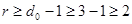

5) Соблюдая условия 1 и 4, находим остатки от деления единицы с нулями на образующий многочлен:

1000000| 1101 Остатки

1101 101

1010 111

1101 011

1110 110

1101

6) Строим образующую матрицу

C_7;4 =

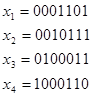
7) Суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы находим остальные комбинации искомого кода (первые четыре комбинации – строки образующей матрицы):

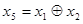
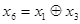
0001101 0001101

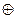
00101110100011

0011010 0101110

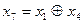
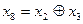
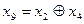
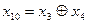0001101 0010111 0010111 0100011

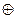
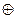
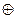
0010111010001110001101000110

0011010 0110100 1010001 1100101

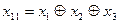
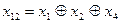
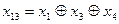
0001101 0001101 0001101

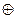0010111 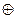0010111 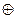0100011

010001110001101000110

0111001 1011100 1101000

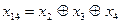
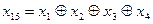
0010111 0001101

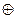0100011 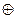0010111

1000110 0100011

1110010 1000110

Задача 6.109. Используя условие предыдущей задачи, построить циклический код при помощи образующего многочлена х³+ х+ 1.

Задача 6.110. При помощи образующей матрицы, полученной в результате умножения строк единичной матрицы на образующий многочлен х³+ х+ 1, построить циклический код, испрааляющий одиночную ошибку в любом из четырех информационных разрядов кода.

Решение. Так как в искомом коде n_и = 4, то единичная мат- рица содержит 4 строки.

Строим образующую матрицу

0001*1011=0001011

0010*1011=0010110

0100*1011=0101100

1000*1011=1011000

Строки образующей матрицы являются первыми четырьмя ком- бииациями искомого кода, т.е.

1) 0001011 2) 0010110 3) 0101100 4) 1011000

Находим остальные комбинации кода суммированием по модулю 2 строк образующей матрицы

5) 0001011 6) 0001011 7) 0001011

001011001011001011000

0011101 0100111 1010011

8) 0010110 9) 0010110 10) 0101100

010110010110001011000

0111010 1001110 1110100

11) 0001011 12) 0001011 13) 0001011

0010110 0101100 0010110

010110010110001011000

0110001 1111111 1000101

14) 0010110 15) 0001011

0101100 0010110

1011000 0101100

1100010 1011000

Сгруппируем полученные коды

1) 0001011 8) 0011101

2) 0010110 9) 0111010

3) 0101100 10) 1110100

4) 1011000 11) 1101001

5) 0110001 12) 1010011

6) 1100010 13) 0100111

7) 1000101 14) 1001110

15) 1111111

Как видим, кодовые комбинации 1 – 15 ничем не отличаютcя от кодов, полученных в задаче 6.103, что подтверждает идентичность методов их получения.

Задача 6.111. Используя многочлен, обратный многочлену x³ + x + 1, построить циклический код дпя передачи ненулевых комбинаций четырехзначного двоичного кода на все сочетания. Образующую матрицу строить умножением единичной матрицы на полученный обратный многочлен.

Задача 6.112. Построить циклический код методом циклического сдвига строки образующей матрицы, полученной в задаче 6.110, и зеркальной ей комбинации.

Решение.

1) 0001011 8) 1110100

2) 0010110 9) 1101001

3) 0101100 10) 1010011

4) 1011000 11) 0100111

5) 0110001 12) 1001110

6) 1100010 13) 0011101

7) 1000101 14) 0111010

15) 1111111

Задача 6.113. Показать процесс исправления одиночной ошибки в принятой кодовой комбинации на примере кода, полученного в задаче 6.110.

Решение. Предположим, передавалась комбинация № 14 и в ней исказился четвертый разряд.Такимобразом, принятая комбинация имеет вид: 1000110.

1) Делим принятую комбинацию на образующий многочлен

1000110| 1011

1011___

1011_

2) Сравниваем вес полученного остатка W с возможным для данного кода числом исправляемых ошибок s. Вес остатка W = 2. Число исправляемых ошибок s = 1; W>s.

3) Производим циклический сдвиг принятой комбинации F(х) на один разряд влево и делим полученную в результате циклического сдвига комбинацию на К (х):

0001101| 1011

1011

4) Повторяем пункт 3) до тех пор, пока не будет :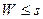

0011010| 1011 0110111| 1011

10111011_

1100 1100

1011 W>s 1011_ W>s

111 1110

1011

1101000| 1011

1011_

1011_

1011_

1010 W=s

1011

5) Складываем по модулю 2 последнее делимое с последним остатком

1101001

6) Производим циклический сдвиг комбинации, полученной в результате суммирования последнего делимого с последним остатком, вправо на 4 разряда (так как перед этим мы четырежды сдвигали принятую комбинацию влево): 1110100, 0111010, 0011101, 1001110, Как видим, последняя комбинация соответствует переданной, т. е. уже не содержит ошибки.

Задача 6.114. При передаче сообщений кодом, построенным в задаче 6.110, в тринадцатой комбинации произошел сбой третьего символа (от начала комбинации). Показать процесс исправления ошибки в принятой комбинации.

Задача 6.115. Обнаружить, какая из трех принятых комбинаций 0011010, 0110100, 1010011 циклического кода, образующий многочлен которого К (х) = х³+ х²+ 1, – ошибочная. Исправить обнаруженную ошибку.

Задача 6.116. Построить циклический код, способный передавать все буквы русского алфавита и исправлять любой одиночный сбой. Показать процесс исправления ошибки.

Задача 6.117. Выбрать образующий многочлен минимально возможной длины для построения циклического кода, обнаруживающего все трехкратные ошибки.

Решение. Для обнаружения нечетного числа ошибок выбираем двучлен (x + 1).

Для обнаружения двукратных ошибок минимальным образующим многочленом будет х³ + x + 1 либо двойственный ему многочлен x³+ x²+ 1 (остальные возможные многочлены будут более высоких степеней, но число ненулевых членов у них будет не меньше, так как оно должно равняться кодовому расстоянию между комбинациями данного кода, в нашем случае – трем).

Минимальными образующими многочленами, обнаруживающими все трехкратные ошибки, будут:

K₁(x) = (x+1)(x³+x²+1) и K₂(x) = (x+1)(x³+x+1)

x³+x²+0+1 x³+0+x+1

______x+1 _____ x+1

x³+x²+0+1 x³+x+0+1

x⁴+x³+0+x__x⁴+0+x²+x__

x⁴+0+x²+x+1 x⁴+x³+x²+0+1

K₁(x)=10111 K₂(x) = 11101

Задача 6.118. Построить образующий многочлен для создания циклического кода, обнаруживающего все трехкратные ошибки, при передаче 1000 сообщений в двоичном коде.

Задача 6.119. Убедиться в том, что код, построенный при помощи двучлена (x + 1), способен обнаруживать любое количество нечетных ошибок.

Решение. Предположим, требуется передать 15 ненулевых комбинаций двоичного кода, т. е. n_и = 4, тогда образующая матрица

0001 * (x + 1) = 00011

0010 *(x + 1) = 00101

0100 * (x + 1) = 01001

1000 *(x + 1) = 10001

Остальные комбинации получим в результате суммирования всевозможных сочетаний строк образующей матрицы. Окончательно код будет иметь вид:

00011 00101 01111

00110 01010 11110

01100 10100 11101

11000 01001 11011

10001 10010 10111

Как видим, полученный код во всех комбинациях содержит четное число единиц. Нарушение условия четности легко обнаруживается при делении принятой комбинации F(x) на образующий двучлен (x+ 1). Остаток будет во всех случаях, когда число ошибок будет нечетным. Аналогично обнаруживаются ошибки и в кодах, имеющих более высокую разрядность. Например, при передаче комбинации 10010 сбои произошли в первом, втором и пятом разрядах, т. е. принятая комбинация F(x) = 01011. Для обнаружения и исправления ошибки делим F(x) на K(x)

01011| 11

11_

11

Получили в остатке 1, тогда как деление правильной комбинации на К (x) остатка не дает:

10010| 11

11_

11_

11

Задача 6.120. Обнаружить пятикратную ошибку в принятом сообщении F(x) = 100011101101011, если известно, что код был построен при помощи двучлена (x + 1).

Задача 6.121. Построить комбинации циклического кода, обнаруживающего трехкратные ошибки при передаче сообщений, составленных из пятизначного двоичного кода на все сочетания.

Решение. Определяем число корректирующих разрядов:

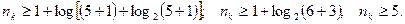
Выбираем из табл. 1 приложения 9 многочлен пятой степени с числом ненулевых членов, большим или равным кодовому расстоянию, т. е. 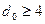, таким многочленом может быть

K(x) = x⁵+x³+x²+x+1

Строим образующую матрицу

00001*101111

00010*101111

00100*101111

01000*101111

10000*101111

C_10;5 =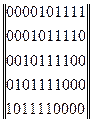

Строки образующей матрицы представляют собой первые 5 комбинаций искомого кода. Остальные комбинации находятся путем суммирования по модулю 2 всевозможных сочетаний строк образующей матрицы.

Задача 6.122. Исходная кодовая комбинация 0101111000, принятая – 0001011001 (т. е. произошел тройной сбой). Показать процесс обнаружения ошибок, если известно, что комбинации исходного кода были образованы при помощи многочлена 101111.

Задача 6.123. Построить все комбинации циклического кода, исправляющего одиночные ошибки в каждой комбинации кода. Число различных комбинаций кода должно обеспечивать передачу 26 букв латинского алфавита. Показать процесс исправления ошибки

в одной из комбинаций, полученной в результате суммирования нескольких строк образующей матрицы.

Решение. Определяем число информационных разрядов

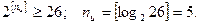
Тогда число корректирующих разрядов

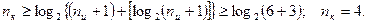
Выбираем образующий многочлен

К(x) =х⁴+х+1=10011.

Строим образующую матрицу

1) 00001*10011

2) 00010*10011

3) 00100*10011

4) 01000*10011

5) 10000*10011

C_{9;5 =}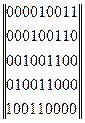

6) a₁ a₂ = 000110101;

7) a₁ a₃ = 001011111;

8) a₁ a₄ = 010001011;

9) a₁ a₅ = 100100011;

10) a₂ a₃ = 101101010;

11) a₂ a₄ = 010111110;

12) a₂ a₅ = 100010110;

13) a₃ a₄ = 011010100;

14) a₃ a₅ = 101111100;

15) a₄ a₅ = 110101000;

16) a₁ a₂ a₃ = 001111001;

17) a₁ a₂ a₄ = 010101101;

18) a₁ a₂ a₅ = 100000101;

19) a₁ a₃ a₄ = 011000111;

20) a₁ a₃ a₅ = 101101111;

21) a₁ a₄ a₅ = 110111011;

22) a₂ a₃ a₄ = 011110010;

23) a₂ a₃ a₅ = 101011010;

24) a₂ a₄ a₅ = 110001110;

25) a₃ a₄ a₅ = 111100100;

26) a₁ a₂ a₃ a₄ = 011100001;

27) a₁ a₂ a₃ a₄ = 101001001;

28) a₁ a₂ a₄ a₅ = 110011101;

29) a₁ a₃ a₄ a₅ = 111110111;

30) a₂ a₃ a₄ a₅ = 111000010;

31) a₁ a₂ a₃ a₄ a₅ = 111010001.

Для передачи 26 букв латинского алфавита можно выбрать любые 25 из полученных 31 комбинации.

Предположим, ошибка произошла в первом разряде при передаче комбинации № 29, т. е. принятая комбинация – 111110110.

Исправляем ошибку

111110110| 10011

10011_

10011_

10111 W=s

10011__

10011

1

Задача 6.124. Проверить возможность исправления ошибки в 30-й и 11-й комбинациях кода, полученного в предыдущей задаче.

Задача 6.125. Показать процесс построения циклического кода для передачи 50 сообщений. Предусмотреть возможность исправления одиночной ошибки и проверить корректирующие способности кода на одной из полученных комбинаций.

Задача 6.126. ”кала прибора имеет 1000 делений. Датчик, преобразующий непрерывные показания прибора в дискретные посылки, реагирует на отклонения стрелки прибора на 1 градацию. Построить циклический код для передачи любого из показаний прибора с точностью до 1 градации, причем кодовое расстояние между комбинациями полученного кода должно быть д) 3. Про- верить корректирующие способности кода.

Решение. 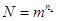, т = 2, N = 1000, n _и = [ log₂ 1000] = 10;

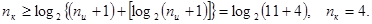
Степень образующего многочлена К(x) равна n_к = 4, число ненулевых членов К (x) равно d₀ =3.

К (x) = x⁴ +x³+ 1 11001.

Строим образующую матрицу методом циклического сдвига комбинации, полученной путем умножения строки единичной матрицы

ранга n _и на образующий многочлен: 0000000001 * 11001 = 00000000011001.

Образующая матрица имеет вид:

С_14;10 =

Остальные комбинации получаем, как обычно, суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы.

Предположим, в комбинации, полученной в результате суммирования первой, второй и седьмой строк образующей матрицы

00000000110010

00011001000000

00011001101011,

искажен третий символ.

Исправляем ошибку

00011001101111 | 11001

11001_____

10111 W>s

11001_

Производим циклический сдвиг на один разряд влево и снова делим на К (x)

00110011011110| 11001

11001_____

11001_

11101 W=s

11001_

1000

Производим циклический сдвиг на один разряд вправо и получаем исправленную комбинацию 00011001101011.

Задача 6.127. Построить, циклический код с d ₀ = 3; s = 1; n _и = 4. Убедиться, что образующую матрицу можно построить путем циклического сдвига образующего многочлена, умноженного на строку единичной матрицы, ранг которой равен n _и. Построенный код сравнить с кодами, полученными в задачах 6.99 и 6. 108.

Задача 6.128. Методом циклического сдвига строки образующей матрицы и зеркальной ей комбинации построить циклический код с d ₀ =З и n _и =5.

Решение. По аналогии с задачей 6.123

К(x) = x⁴+x+ 1 10011.

Первая строка образующей матрицы 000010011.

Комбинации искомого циклического кода: 1) 000010011 2) 000100110 3) 001001100 4) 010011000 5) 100110000 6) 001100001 7) 011000010 8) 110000100 9) 100001001 10) 111101100 (первая зеркальная комбинация) 11) 111011001 12) 110110011 13) 101100111 14) 011001111 15) 110011110 16) 100111101 17) 001111011 18) 011110110

Задача 6.129. Строка образующей матрицы имеет вид: 00000000110010. Построить все возможные комбинации циклического кода, если никаких других параметров кода не задано,

Задача 6.130. Построить циклический код длиной в 15 символов, исправляющий одну или две ошибки.

Решение. Согласно (79), и = 2^h – 1, откуда

h = log₂ (n + 1) = log₂ 16 = 4.

Число контрольных символов

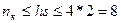
Порядок старшего из минимальных многочленов

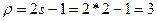
Количество минимальных многочленов, участвующих в построении образующего многочлена,

L=s=2

а старшая степень

l=h=4

Степень образующего многочлена

.

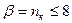Из колонки 4 табл. 2 приложения 9, где расположены минимальные многочлены степени l = 4, выбираем два (L = 2) минимальных многочлена, порядок старшего из которых равен 3 (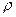 =3), т.е выбираем минимальные многочлены 1 и 3. Тогда

K(x)=M₁(x)*M₃(x) = 10011*11111=111010001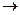

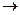x⁸ + x⁷ + x⁶ + x⁴ + 1

Число информационных разрядов

n_и = n - n_к = 15 – 8 = 7.

Образующая матрица кода (15; 7)

С_15;7 =

Остальные комбинации кода получаются суммированием всевозможных сочетаний строк образующей матрицы.

Задача 6.131. Построить код БЧХ с п = 31 и s = 2.

Задача 6.132. Построить циклический код, способный исправлять двойную ошибку, если требуемая длина кода n = 21.

Решение. 1) Определяем значение h

h = log₂ (п + 1)

или, согласно (81), для больших n

h = log₂ (п * C + 1)

при атом h всегда должно быть целым числом;

h = log₂ (21 * C + 1)

откуда С = 3, так как ближайшее число, которое в сумме с 1 дает целую степень двух, будет 63. Окончательно,

h = log₂ (21 * 3 + 1) = 6

2) ;

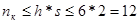3) ;

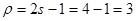4) L=s= 2;

5) ;

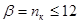6) l=h= 6;

7) Из колонки 6 (l = 6) табл. 2 приложения 9 выписываем два (L = 2) минимальных многочлена, порядок старшего из которых равен 3 (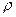 = 3), т. е. выбираем многочлены М₁ (x) и М₃ (x).

8) Умножаем индексы выбранных многочленов на С и окончательно получаем порядковые номера минимальных многочленов, из которых строим образующий многочлен:

М₃ (x) и М₉(x) т. е. 1010111 и 1101.

K(x)=M₃(x)*M₉(x)=(x⁶+x⁴+x²+x+1)(x³+x²+1);

K(x)= 1010111 * 1101 = 1110110011 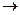x⁹+x⁸+x⁷+x⁵+x⁴+x+1.

9) Так как степень выбранного многочлена 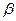=9, то уточненное значение числа корректирующих разрядов n_к = 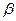=9;

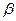=ls; n_н = n-n_к = 21 – 9 = 12,

Таким образом, первая строка образующей матрицы имеет вид

000000000001110110011.

Образующая матрица и дальнейший код строятся одним из методов, описанных в общей методике.

Задача 6.133. Приемно-передающая аппаратура обеспечивает прием и передачу блоков длиной n = 63. Построить циклический код, исправляющий пятикратные ошибки.

Задача 6.134. Показать процесс исправления двойной ошибки в БЧ" коде (15; 7) (см. задачу 6.130).

Решение. Возьмем комбинацию, полученную в результате суммирования 3 и 7 строк образующей матрицы

111010001000000

Полученная комбинация принадлежит коду (15; 7), образующая матрица которого построена в задаче 6.130, так как одним из свойств циклического кода является тот факт, что сумма по модулю 2 любых двух комбинаций кода является также комбинацией того же кода.

Рассмотрим теперь три варианта: I. Ошибки расположены рядом, пусть ошибочными будут второй и третий разряды кода. II. Ошибочные разряды расположены не рядом, пусть ошибочными являются первый и пятый разряды кода. III. Ошибки расположены не рядом, пусть в этом случае ошибочными будут четвертый и девятый разряды.

Вариант 1. Как обычно, делим искаженную комбинацию на образующий многочлен:

111001100000010| 111010001

111010001____

111010000 W=s

111010001__

110

111001100000100 - исправленная комбинация.

Вариант 2.

111001100010101| 111010001

111010001____

111010101 W=s

111010001__

10001

111001100000100 - исправленная комбинация

Вариант 3.

111001000001100| 111010001

111010001____

111010001___

100001000 W>s

111010001

110010000011001| 111010001

111010001__

111010001_

110101001 W>s

111010001__

111010001_

100100000110011| 111010001

111010001_

111010001___

111010001__

100010111 W>s

111010001

001000001100111| 111010001

111010001_

111010001__

111111111 W>s

111010001_

010000011001110| 111010001

111010001_

111010001___

111111111 W>s

111010001__

100000110011100| 11101001

111010001_

111010001__

111111111 W>s

111010001

111010001

000001100111001| 111010001

111010001_

10011011 W>s

100111001000001| 111010001

111010001_

111010000 W=s

111010001_____

100001

Производим 12-кратный циклический сдвиг вправо комбинации, полученной в результате сложения по модулю 2 последнего делимого и последнего остатка, либо трехкратный сдвиг влево той же комбинации. Полученная после соответствующего числа циклических сдвигов комбинация не содержит ошибок – 111001100000100.

Задача 6.135. Показать процесс исправления двукратной ошибки в коде, полученном в задаче 6.132.

Задача 6.136. Построить циклический код, исправляющий трехкратную ошибку, при общей длине кода n = 15 символов. Убедиться в возможности исправления трехкратных ошибок в полученном коде.

Задача 6.137. Построить циклический код, способный исправлять шестикратную ошибку при общей длине кода и = 63. Показать процесс исправления шестикратной ошибки,

Решение. 1) Определяем h, так как

N = 2^h – 1, то 63 = 2^h – 1; h = log₂64 = 6.

2) Порядок старшего из выбираемых минимальных многочленов

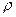= 2 s – 1 = 11.

3) Количество минимальных многочленов, участвующих в построении образующего многочлена,

L = s = 6,

а старшая степень

l = h = 6.

4) Из колонки 6 табл. 2 приложения 9 выписываем шесть мини- мальных многочленов, порядок старшего из которых 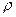= 11, т. е.

M₁ – 1000011; M₃ – 1010111; M₅ – 1100111; M₉ – 1101; M₁₁ – 1101101.

5) Строим образующий многочлен

1010111 * 1100111 * 1001001 * 1000011 * 1101 * 1101101 =

= 1101111100110100001110101101100111 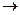x³³ + x³² + x³⁰ + x²⁹ + x²⁸ + x²⁷ + x²⁶ + x²³ + x²² + x²⁰ + x¹⁵ + x¹⁴ + x¹³ + x¹¹ + x⁹ + x⁸ + x⁶ + x⁵ + x² + x + 1;

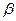<l*5, n_к=33, n_и = 63 – 33 =- 30, код (63; 30).

6) Так как сумма по модулю 2 двух любых комбинаций циклического кода также является комбинацией того же хода, то в качестве проверочной возьмем комбинацию, полученную суммированием первых двух строк образующей матрицы

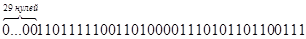
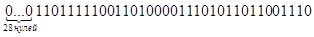
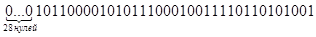
7) Предположим, искаженными оказались 2, 3, 5, 6, 8 и 10-й символы, для исправления ошибки делим искаженную комбинацию на К (x) 28 нулей

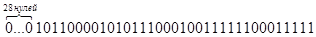| K(x)

1101111100110100001110101101100111_

1101111100110100001110100111010001

1101111100110100001110101101100111

Складываем делимое с остатком и получаем исправленную комбинацию

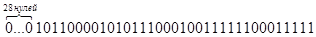
1010110110

0…010110000101011100010011110110101001

Задача 6.138. Построить код БЧ", способный исправить 14- кратную ошибку при общей длине кода n = 63. Проверить корректирующие способности кода.