Причины теплового расширения можно понять, если учесть влияние ангармонических членов в выражении для потенциальной энергии взаимодействия пар атомов при температуре Т (рис. 3.5):
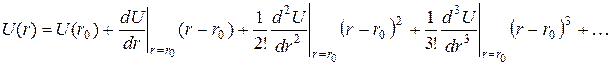
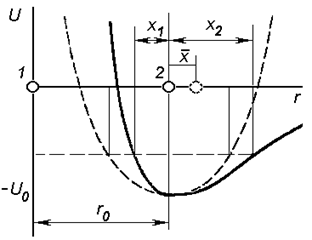 |
| Рис. 3.5. Зависимость потенциальной энергии взаимодействия частиц от расстояния между ними |
Введем следующие обозначения: 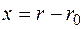 – смещение атома из его положения равновесия
– смещение атома из его положения равновесия 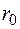 при 0 К,
при 0 К,
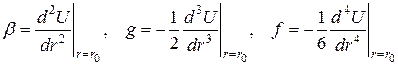
и учтем, что 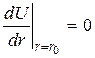 . Тогда выражение для потенциальной энергии примет вид
. Тогда выражение для потенциальной энергии примет вид
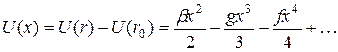 (3.37)
(3.37)
Член с 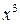 описывает асимметрию взаимного отталкивания атомов, член с
описывает асимметрию взаимного отталкивания атомов, член с  – сглаживание колебаний при больших амплитудах.
– сглаживание колебаний при больших амплитудах.
При абсолютном нуле атомы располагаются на расстояниях 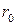 , что соответствует минимуму энергии взаимодействия
, что соответствует минимуму энергии взаимодействия 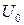 (у дна потенциальной ямы). С повышением температуры атомы начинают колебаться около положения равновесия. Для упрощения предположим, что атом 1 закреплен неподвижно и колеблется лишь атом 2.
(у дна потенциальной ямы). С повышением температуры атомы начинают колебаться около положения равновесия. Для упрощения предположим, что атом 1 закреплен неподвижно и колеблется лишь атом 2.
Если бы атом 2 совершал чисто гармонические колебания, то сила, которая возникает при отклонении его от положения равновесия на расстояние x, была бы строго пропорциональна этому отклонению и направлена к положению равновесия. Потенциальная энергия 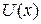 атома описывалась бы при этом квадратичной параболой
атома описывалась бы при этом квадратичной параболой 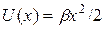 (штриховая кривая на рис.3.5). Эта парабола симметрична относительно прямой, которая проходит через
(штриховая кривая на рис.3.5). Эта парабола симметрична относительно прямой, которая проходит через 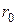 . Поэтому отклонения
. Поэтому отклонения 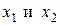 были бы одинаковыми по величине, и центр смещения совпадал бы с положением равновесия, то есть с точкой
были бы одинаковыми по величине, и центр смещения совпадал бы с положением равновесия, то есть с точкой 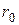 .
.
В действительности колебания не являются гармоническими, что связано с несимметричным характером потенциальной энергии (сплошная кривая на рис.3.5). Это обстоятельство приводит к тому, что отклонение атома 2 вправо и влево оказываются неодинаковыми: вправо частица отклоняется сильнее, чем влево. В результате этого среднее положение частицы 2 уже не совпадает с положением равновесия 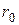 , а смещается вправо.
, а смещается вправо.
Среднее смещение 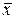 можно вычислить, если воспользоваться функцией распределения Больцмана[6], с помощью которой усреднение возможных значений какой-нибудь физической величины осуществляется в соответствии с их термодинамическими вероятностями
можно вычислить, если воспользоваться функцией распределения Больцмана[6], с помощью которой усреднение возможных значений какой-нибудь физической величины осуществляется в соответствии с их термодинамическими вероятностями
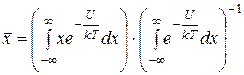 (3.38)
(3.38)
Полагая смещение таким, что ангармонические члены в выражении для энергии можно считать малыми по сравнению с 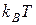 , подынтегральные функции раскладываем в ряд:
, подынтегральные функции раскладываем в ряд:
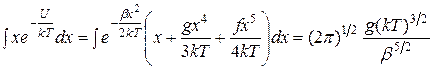 , (3.39)
, (3.39)
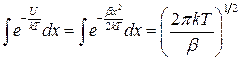 , (3.40)
, (3.40)
и поэтому
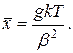 (3.41)
(3.41)
Коэффициент теплового расширения (КТР) равняется относительному изменению 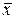 при нагревании тела на 1 К
при нагревании тела на 1 К
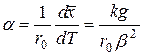 . (3.42)
. (3.42)
Значения КТР для некоторых металлов приводятся в таблице 3.3.
Определим зависимость КТР от температуры. Средняя величина полной энергии атома определяется среднеквадратичным смещением: 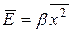 . Среднее во времени значение силы, которая действует на атом, должно равняться нулю:
. Среднее во времени значение силы, которая действует на атом, должно равняться нулю: 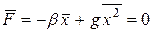 . Следовательно,
. Следовательно, 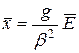 . Подставляя полученное значение
. Подставляя полученное значение 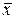 в (3.42), получаем
в (3.42), получаем
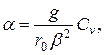 (3.43)
(3.43)
где 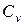 — теплоемкость, отнесенная к одному атому.
— теплоемкость, отнесенная к одному атому.
Таблица 3.3. Коэффициенты линейного теплового расширения в области комнатной температуры
| Вещество |  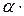 106, град-1 106, град-1 | Вещество | 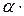 106, град-1 106, град-1 |
| Li Cs Cu Ag Au Al | Pb Fe Ni Cr Mo W | 11,7 12,5 7,5 5,2 4,6 |
Из (3.43) следует, что КТР твердых тел пропорционален теплоемкости и с температурой он должен изменяться так же, как изменяется теплоемкость (рис.3.6). Из физики твердого тела известно, что коэффициент ангармоничности 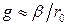 . Подставляя это выражение в (3.43), получаем
. Подставляя это выражение в (3.43), получаем
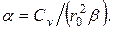 (3.44)
(3.44)
Следовательно, КТР обратно пропорционален коэффициенту жесткости связи 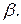 Поэтому он низкий для кристаллов с сильными, например, ковалентными связями (
Поэтому он низкий для кристаллов с сильными, например, ковалентными связями (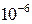 град-1), и высокий для кристаллов со слабыми, в частности, молекулярными связями (до
град-1), и высокий для кристаллов со слабыми, в частности, молекулярными связями (до 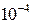 град-1).
град-1).
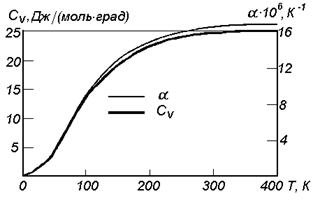 |
| Рис. 3.6. Зависимость коэффициента линейного расширения от температуры |
Зависимость КТР от 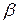 позволяет целенаправленно изменять его путем изменения жесткости связи. Этим пользуются, например, для получения стекол с различными КТР путем введения в силикатную основу окислов металлов. За счет взрыхления структуры стекла можно добиться изменения КТР на два порядка. Для металлов изменения КТР в таких же границах можно получить, сплавляя их друг с другом.
позволяет целенаправленно изменять его путем изменения жесткости связи. Этим пользуются, например, для получения стекол с различными КТР путем введения в силикатную основу окислов металлов. За счет взрыхления структуры стекла можно добиться изменения КТР на два порядка. Для металлов изменения КТР в таких же границах можно получить, сплавляя их друг с другом.
 2015-03-22
2015-03-22 1548
1548








