1. Изохорный процесс (V = const)
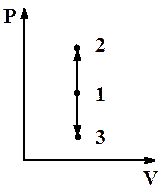 Рис.2.8. Изохорный процесс Рис.2.8. Изохорный процесс | Диаграмма этого процесса (рис.2.8) – изохора – в координатах (P,V) изображается прямой, параллельной оси ординат (ось P). Процесс 1-2 – изохорный нагрев, процесс 1-3 – изохорное охлаждение. При изохорном процессе газ не совершает работу над внешними телами  и вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии и вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии 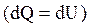 . Поскольку . Поскольку 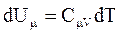 , то для произвольной массы газа , то для произвольной массы газа |
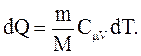 (2.46)
(2.46)
2. Изобарный процесс (P = const)
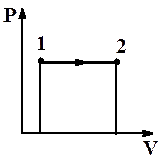 Рис.2.9. Изобарный процесс Рис.2.9. Изобарный процесс | Диаграмма этого процесса (рис.2.9) – изобара – в координатах (P,V) изображается прямой, параллельной оси абсцисс (ось V). При изобарном процессе работа газа при увеличении объема от V1 до V2 равна: 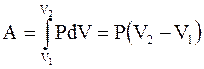 (2.47) и определяется площадью прямоугольника под прямой 1-2. (2.47) и определяется площадью прямоугольника под прямой 1-2. |
Используя уравнение Менделеева-Клапейрона, получим:
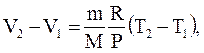
отсюда
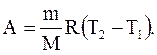 (2.48)
(2.48)
Физический смысл универсальной газовой постоянной: R численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1 К.
3. Изотермический процесс (T = const)
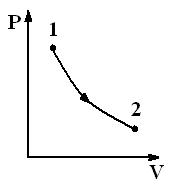 Рис.2.10. Изотермический процесс Рис.2.10. Изотермический процесс | Диаграмма этого процесса (рис.2.10) – изотерма – в координатах (P,V) представляет собой гиперболу. Изотермический процесс описывается законом Бойля-Мариотта (PV = const). Работа изотермического расширения газа |
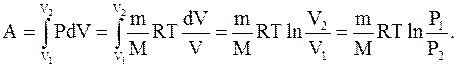 (2.49)
(2.49)
Так как при T = const внутренняя энергия идеального газа не изменяется, то из первого начала термодинамики следует, что 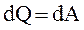 , то есть все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил.
, то есть все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил.
Поэтому для того, чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.
4. Адиабатический процесс (dQ = 0)
Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой (dQ = 0).
К адиабатическим процессам можно отнести все быстропротекающие процессы (теплообмен не успевает совершиться), например, распространение звука в среде, циклы расширения и сжатия в двигателях внутреннего сгорания, в холодильных установках и т.д.
Из первого начала термодинамики следует, что при адиабатическом процессе 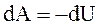 . Используя
. Используя 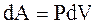 и
и 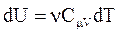 , получим:
, получим:
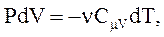 (2.50)
(2.50)
с другой стороны, из 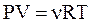 следует:
следует:
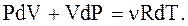 (2.51)
(2.51)
Разделив (2.51) на (2.50), получим:
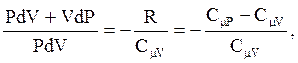
или
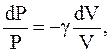 (2.52)
(2.52)
где 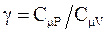 - коэффициент Пуассона.
- коэффициент Пуассона.
Проинтегрируем (2.52):
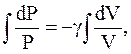
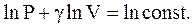
Потенциируя последнее выражение, получим уравнение Пуассона:
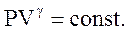 (2.53)
(2.53)
Используя уравнение Менделеева-Клапейрона, получим:
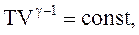 (2.54)
(2.54)
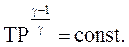 (2.55)
(2.55)
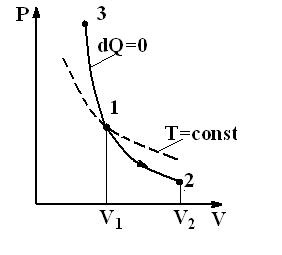 Рис.2.11. Адиабата и изотерма Рис.2.11. Адиабата и изотерма | Диаграмма адиабатического процесса (адиабата) в координатах (P,V) изображается гиперболой (рис.2.11). Адиабата (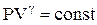 ) более крутая, чем изотерма ( ) более крутая, чем изотерма (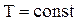 ). Это объясняется тем, что при адиабатическом сжатии (3-2) увеличение давления газа обусловлено не только уменьшением его объема, но и повышением температуры. ). Это объясняется тем, что при адиабатическом сжатии (3-2) увеличение давления газа обусловлено не только уменьшением его объема, но и повышением температуры. |
В адиабатическом процессе 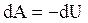 , поэтому
, поэтому 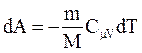 . Если газ адиабатически расширяется от объема V1 до V2, то его температура уменьшается от T1 до T2 и работа расширения идеального газа
. Если газ адиабатически расширяется от объема V1 до V2, то его температура уменьшается от T1 до T2 и работа расширения идеального газа
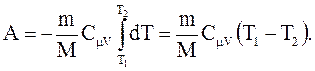 (2.56)
(2.56)
Откуда, используя уравнение Менделеева-Клапейрона, получаем:
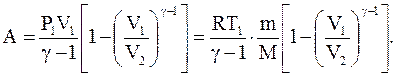
Работа адиабатического расширения 1-2 (рис.2.11, область под кривой 1-2) меньше, чем при изотермическом процессе. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.
 2015-03-27
2015-03-27 869
869








