Слово ωÎVk называется еще цепочкой ω. Длина цепочки обозначается |ω|.
При k=0 получаем пустое слово, обозначаемое l. |l|=0.
V* – множество всех слов – эквивалент универсума в теории множеств.
Нетрудно видеть, что V* счетно. Пусть V={а,b}. Будем нумеровать слова [4]: а=1, b=2, аа=3=(1×21+1×20), аb=4=(1×21+2×20), bа=5=(2×21+1×20), bb=6=(2×21+2×20) и т.д. Получилась так называемая лексико-графическая нумерация. Таким образом, по каждой цепочке можно получить ее номер. У пустой цепочки номер 0. По номеру можно получить цепочку в заданном алфавите.
Пусть V={а,b,с}. Получим цепочку №20. Предварительно введем таблицу формирования номера в таком алфавите (табл. 89).
Таблица 89
Формирование номера цепочки в V={а,в,с}
| а | ||||
| b | ||||
| с | ||||
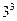
| 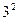
| 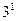
| 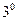
|
Тогда 20=9+9+2, то есть (1×32+3×31+2×30), получаем цепочку асb.
Подобным образом можно нумеровать и другие объекты. Получим, например, номер формулы логики высказываний А®В. Алфавит: {А,В,®,¯}, тогда номер цепочки: (1×32 +3×31+2×30)=20.
В этой цепочке старший (левый) разряд А, номер символа А в алфавите равен 1, вес его =32; следующий символ ®, номер символа ® равен 2, вес его =31; младший (правый) символ В, номер символа В равен 3, вес =30. Ясно, что не все номера представляют собой правильные формулы. Например, формула ®АВ – неправильная. Хотя в случае использования так называемой префиксной формы записи (символ бинарной операции ставится перед символами переменных – это польская инверсная запись ПОЛИЗ) эта формула будет правильной.
Получим номер автомата – распознавателя последовательности 0132 в алфавите {0,1,2,3}:
(1×33+2×32+4×31 +3×30)=60.
Получим номер алгоритма по его логической схеме: 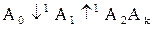 в алфавите {
в алфавите { 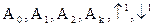 }:
}: 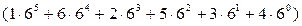 =16186.
=16186.
Получим номер модуса Barbara в виде ааа1 (1 – номер фигуры) в алфавите {a,i,e,o,1,2,3,4}, где буква – вид суждения, цифра – номер модуса:
(1×83+1×82+1×81 +5×80)=589.
Над цепочками вводятся операции, например:
· конкатенации ½½ (сцепления), например, аb½½bc=аbbс;
· итерации * (повторения), например: а(bbа)*=аbbаbbаbbа…;
· инверсии  (реверса), например,
(реверса), например, 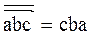 ;
;
· циклического сдвига W (циклической перестановки символов), например, влево: W(аbс)=bса, или вправо: (аbс)W=саb;
· перестановки групп символов (подцепочек данной цепочки), например, Q(ав(вс)(ав))=ававвс;
· замены одной подцепочки данной цепочки другой цепочкой: (аbbс,bbÞd)=adc.
Ранее мы упоминали о генетических алгоритмах. В них цепочками представляются некоторые варианты решения комбинаторной задачи. Такие цепочки называют как в генетике – хромосомами. В процессе «скрещивания» двух хромосом образуется новая хромосома, то есть цепочка, состоящая из частей «родительских» цепочек. В дальнейшем в процессе «эволюции» остаются или «выживают» только самые жизнеспособные, т.е. лучшие варианты. Так происходит и в природе. Все мы носим эти цепочки хромосом с собой и, возможно, передадим их частички в будущее. Не будем забывать заветы великого Дарвина: «Выживает сильнейший», в смысле – умнейший. Хотя, точнее, – тот, кто приспосабливается к изменениям.
 2015-03-27
2015-03-27 707
707








