В математической логике доказывается, что исчисление предикатов непротиворечиво – т.е. в нем невозможно одновременно вывести 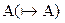 , и
, и 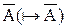 . Кроме того, в силу теоремы Гёделя о полноте исчисления предикатов общезначимая формула выводима в исчислении предикатов.
. Кроме того, в силу теоремы Гёделя о полноте исчисления предикатов общезначимая формула выводима в исчислении предикатов.
Рассмотренное исчисление предикатов – исчисление предикатов первого порядка. В исчислениях второго порядка возможны кванторы по предикатам, т.е. выражения вида "Р(Р(х)), или по функциям.
Итак, множество всех истинных высказываний логики высказываний перечислимо и разрешимо. Множество всех истинных высказываний логики предикатов перечислимо (ввиду его полноты), но неразрешимо (ввиду бесконечности предметной области).
В качестве еще одной формальной теории в математической логике рассматривается так называемая формальная арифметика, предложенная итальянским математиком Джузеппе Пеано (1858-1932 гг.) [26]. Пеано ввел символы и операции Î, U, I и впервые излагал логику как математическую дисциплину. Впервые попытка сведения математики к логике была предпринята немецким математиком и логиком Готтлибом Фреге (1848-1925 гг.). Это он определил множество, как объем понятия. Он писал: «Арифметика есть часть логики и не должна заимствовать ни у опыта, ни у созерцания никаких основ доказательств». Знаменитый парадокс о множестве всех множеств – это противоречие в системе Фреге, выявленное Бертраном Расселом.
Гёдель доказал, что любая формальная теория Т, содержащая формальную арифметику, неполна: в ней существует замкнутая формула F, такая, что 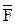 истинно, но ни F, ни
истинно, но ни F, ни 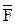 не выводимы в Т. В соответствии со знаменитой теоремой Гёделя о неполноте, для любой непротиворечивой формальной теории Т, содержащей формальную арифметику, формула, выражающая непротиворечивость Т, недоказуема в Т.
не выводимы в Т. В соответствии со знаменитой теоремой Гёделя о неполноте, для любой непротиворечивой формальной теории Т, содержащей формальную арифметику, формула, выражающая непротиворечивость Т, недоказуема в Т.
Таким образом, арифметика и теория чисел являются неаксиматизируемыми теориями, а множество всех истинных высказываний арифметики неперечислимо.
Теоремы Гёделя имеют важное методологическое значение [19]. Оказывается, для достаточно богатых математических теорий не существует адекватных формализаций. Правда, любую неполную теорию Т можно расширить, добавив к ней в качестве аксиомы истинную, но не выводимую в Т формулу, однако, новая теория также будет неполна. Кроме того, невозможно исследовать метасвойства теории средствами самой формальной теории, т.е. всякая метатеория Т для того, чтобы иметь возможность доказывать хотя бы непротиворечивость, должна быть богаче Т [19].
Таким образом, под сомнение берется сам подход построения математики как некоторой фиксированной совокупности средств, которые можно было бы объявить единственно законными и с их помощью строить метатеории любых теорий. Но это вовсе не крах формального подхода. Наличие неразрешимых проблем не говорит о том, что конструктивный подход не пригоден, если он чего-то и не может, то лишь потому, что этого не может никто [19].
Невозможность полной формализации содержательно определенных теорий – это не недостаток концепции, а объективный факт, неустранимый никакой концепцией.
Невозможность адекватной формализации теории означает, что надо либо искать формализуемые ее фрагменты, либо строить более сильную формальную теорию, которая, правда, снова будет неполна, но, быть может, будет содержать всю исходную теорию [19].
 2015-03-27
2015-03-27 648
648








