Условие: Студенческие отряды СО-1, СО-2 и СО-3 численностью 70, 99 и 80 человек принимают участие в сельскохозяйственных работах. Для уборки картофеля на полях П1, П2, П3 и П4 необходимо выделить соответственно 47, 59, 49 и 43 человека. Производительность труда студентов зависит от урожайности картофеля, от численности отряда и характеризуется для указанных отрядов и полей в центнерах на человека за рабочий день и представлена в матрице:
Сумма = 198
| Bj Ai | П1 | П2 | П3 | П4 | |
| СО-1 | 3 | 7 | 2 | 5 | |
| СО-2 | 2 | 3 | 4 | 6 | |
| СО-3 | 6 | 4 | 3 | 5 |
Сумма = 249
Требуется:
1) Распределить студентов по полям так, чтобы за рабочий день было собрано максимально возможное количество картофеля;
2) Определить, сколько центнеров картофеля будет убрано с четырех полей при оптимальном распределении студентов
Решение:
1.Проверяем задачу на сбалансированность.
Общее количество человек в студенческих отрядах на 51 больше требуемого общего количества человек для уборки картофеля.
Задача является не сбалансированной.
Чтобы сбалансировать задачу, добавляем фиктивное картофельное поле, для уборки которого нужно выделить 51 человека. Производительность труда студентов на фиктивном поле принимаем равной НУЛЮ.
Составляем исходную таблицу
табл.1
Сумма = 249
| Bj Ai | П1 | П2 | П3 | П4 | П5 | |
| СО-1 | 3 | 7 | 2 | 5 | 0 | |
| СО-2 | 2 | 3 | 4 | 6 | 0 | |
| СО-3 | 6 | 4 | 3 | 5 | 0 |
Сумма = 249
Обозначения:
П5 – фиктивное картофельное поле;
Сij – производительность труда студентов i -го СО на j – м картофельном поле;
Xij – количество студентов, направляемое из i -го СО на j-ое картофельное поле;
Ui – условные оценки СО;
Vj – условные оценки картофельных полей
Составляем математическую модель прямой и двойственной задач.
Математическая модель прямой задачи :
Целевая функция (на максимум)
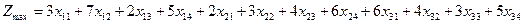
Система ограничений:
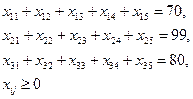 | 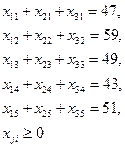 |
 2015-03-27
2015-03-27 1007
1007








