Расчет сетевых графиков

На рис. 2 показана одна дуга сетевого графика со всеми величинами, необходимыми для расчета и получаемыми в результате его.

t^p_i Rⁿ_ij,R⁴_ij t^p_j

tⁿ_i t_ij tⁿ_j

Обозначения:

i – код начального события работы;

j – код конечного события работы;

ij – код работы (дуги);

t_ij – продолжительность работы ij;

t^р_i – ранний срок свершения i-го события, самый ранний срок, в который событие может произойти;

t^p_j – ранний срок свершения j-го события;

tⁿ_i – поздний срок свершения i-го события, - самый поздний допустимый срок свершения, при котором общая продолжительность работ по графику не увеличится;

tⁿ_j – поздний срок свершения j-го события;

t^p^н_ij – раннее начало работы ij;

t^po_ij – раннее окончание работы ij;

tⁿ^н_ij – позднее начало работы ij;

t^no_ij – позднее окончание работы ij;

Rⁿ_ij – полный резерв времени работы, время, на которое можно задержать окончание работы, но так, чтобы при это общая продолжительность работ по графику не увеличилась;

R^ч_ij – частный резерв работы, - время, на которое можно задержать окончание работы так, чтобы ранний срок свершения события j не увеличился.

Алгоритм расчета сетевого графика.

1. Для начального события 1 назначается t^p₁=0.

2. Достигаемая от начального события графика к конечному. Последовательно просматриваются события в порядке возрастания их кодов и вычисляются ранние сроки свершения событий по формуле t^p_j=max(t^p_i+t^p_j). Если в событие j входит несколько дуг, то по каждой их них вычисляется величина t^p_i+t_ij и в качестве t^p_j принимается большая из рассчитанных величин.

3. Для конечного события графика (код его обозначим k) назначается tⁿ_k=t^p_k – поздний срок свершения конечного события равен раннему сроку свершения этого события.

4. Двигаемся от конечного события графика к начальному. Просматриваются события в порядке убывания их кодов и вычисляются поздние сроки свершения событий по формуле: tⁿ_i=min(tⁿ_j-t_ij). Если из события i выходит несколько дуг. То по каждой их них вычисляется величина tⁿ_j-t_ij и в качестве tⁿ_j принимается меньшая. Если расчет произведен без ошибок, то для начального события графика должно оказаться tⁿ₁=0.

5. Формулы для вычислений по работам:

t^pn_ij=t^p_i; t^no_ij=tⁿ_j;

t^po_ij=t^p_i+ t_ij; Rⁿ_ij= tⁿ_j- t^p_i- t_ij;

tⁿ^н_ij₌ tⁿ_j- t_ij; R^ч_ij= t^p_j- t^p_i- t_ij.

Можно ограничится расчетом на графике. Иногда результаты расчета показывают в таблице.

i	j	t_ij	t^pn_ij	t^po_ij	tⁿ^н_ij	t^no_ij	Rⁿ_ij	R^ч_ij

На рис. 3 показан график с рассчитанными сроками свершения событий. Ранние сроки пишутся над событиями, поздние сроки – под событиями. Критический путь показан двойной линией.

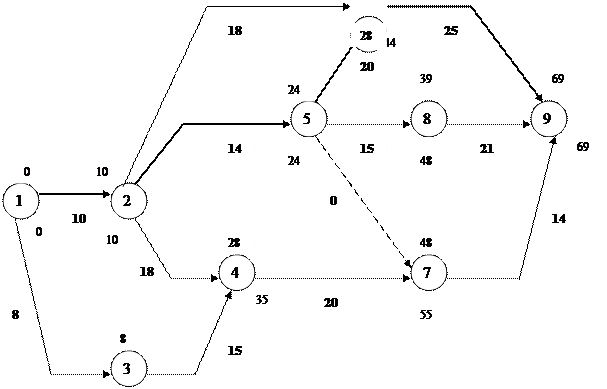В следующей таблице показаны результаты графика:

Работа	t_ij	Р.Н.	Р.О.	П.Н.	П.О.	Резерв	R^ч_ij
i	J	t^pn_ij	t^po_ij	tⁿ^н_ij	t^no_ij	Rⁿ_ij
(1	2)
(1	3)
(2	4)
(2	5)
(2	6)
(3	4)
(4	7)
(5	6)
(5	7)
(5	8)
(6	9)
(7	9)
(8	9)

После упорядочения сетевого графика для наглядности рекомендуется дополнить его линейной диаграммой.

В ней критическое время комплекса работ равно координате на оси времени самого правого конца всех отрезков диаграммы.

Пример задачи.

Дан перечень работ и время выполнения каждой работы. Составить сетевой график и определить сколько всего времени понадобится на выполнение всех работ.

Решение.

1. Составляется сетевой график.

2. Составляется таблица и рассчитываются критические работы и определяются резервы времени.

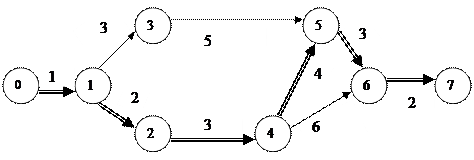Работа	t_ij	Р.Н.	Р.О.	П.Н.	П.О.	Резерв
(ij)	t^pn_ij	t^po_ij	tⁿ^н_ij	t^no_ij	Rⁿ_ij
(0,1)						0
(1,2)						0
(1,3)
(2,4)						0
(3,5)
(4,5)						0
(4,6)
(5,6)						0
(6,7)						0