2.1 Поверхностное натяжение жидкости
На молекулы жидкости, находящейся в поверхностном слое, действуют нескомпенсированные направленные внутрь силы притяжения со стороны остальной части жидкости. При этом величина потенциальной энергии частиц поверхностного слоя превышает величину потенциальной энергии частиц внутри жидкости. Для изотермического перехода молекул изнутри жидкости на её поверхность нужно совершать работу 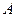 по преодолению направленных внутрь жидкости сил внутреннего давления. Величина
по преодолению направленных внутрь жидкости сил внутреннего давления. Величина 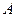 рассчитывается по формуле
рассчитывается по формуле
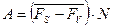 . (2.1)
. (2.1)
В выражении (2.1):
- 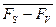 – средняя разность свободных энергий на поверхности
– средняя разность свободных энергий на поверхности 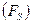 и в объёме
и в объёме 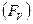 жидкости;
жидкости;
- 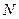 – число молекул в поверхностном слое жидкости.
– число молекул в поверхностном слое жидкости.
При обратном переходе молекулы жидкости с поверхности вглубь её потенциальная энергия переходит в кинетическую. Таким образом, молекулы поверхностного слоя жидкости обладают дополнительной потенциальной энергией. При увеличении размеров капли жидкости её объём возрастает как куб, а площадь поверхности – как квадрат линейных размеров. Поэтому из-за наличия поверхностной энергии жидкость обнаруживает стремление к уменьшению площади своей поверхности. Сокращение площади поверхности капли действует на участки жидкости, с которыми эта поверхность граничит, с силами, называемыми силами поверхностного натяжения 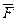 . Вектор
. Вектор 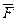 направлен по касательной к поверхности жидкости и перпендикулярен участку жидкости, на который действует сила
направлен по касательной к поверхности жидкости и перпендикулярен участку жидкости, на который действует сила 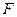 .
.
Пусть 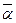 – это сила поверхностного натяжения, приходящаяся на единицу длины
– это сила поверхностного натяжения, приходящаяся на единицу длины 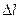 . Эту величину называют коэффициентом поверхностного натяжения:
. Эту величину называют коэффициентом поверхностного натяжения:
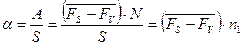 . (2.2)
. (2.2)
В выражении (2.2):
- 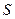 – площадь поверхности жидкости;
– площадь поверхности жидкости;
- 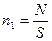 – число молекул на поверхности площади жидкости.
– число молекул на поверхности площади жидкости.
Коэффициент 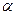 имеет единицы измерения ньютон на метр [Н/м]. Значение коэффициента
имеет единицы измерения ньютон на метр [Н/м]. Значение коэффициента 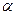 зависит от природы жидкости, температуры и других факторов.
зависит от природы жидкости, температуры и других факторов.
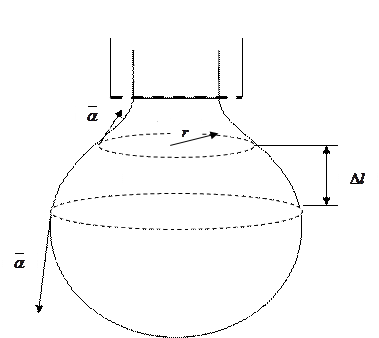
Рассмотрим процесс нарастания объёма капли (рисунок 2.1). Перед отрывом капля висит на «шейке». Форма шейки – цилиндрическая. При увеличении линейного размера «шейки» 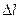 сила тяжести совершает работу
сила тяжести совершает работу
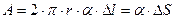 . (2.3)
. (2.3)
В выражении (2.3) величина 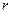 является радиусом «шейки» капли жидкости. Приращение внутренней энергии жидкости
является радиусом «шейки» капли жидкости. Приращение внутренней энергии жидкости 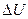 будет равно
будет равно
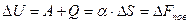 . (2.4)
. (2.4)
 В выражении (2.4) величина
В выражении (2.4) величина 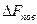 – это приращение свободной энергии
– это приращение свободной энергии 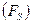 на поверхности жидкости.
на поверхности жидкости.
Рисунок 2.1 – Процесс нарастания объёма капли жидкости
При увеличении температуры 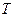 величина поверхностного натяжения
величина поверхностного натяжения 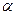 уменьшается. При достижении величины температуры некоторого критического значения
уменьшается. При достижении величины температуры некоторого критического значения 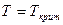 коэффициент поверхностного натяжения
коэффициент поверхностного натяжения 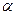 становится равным нулю. При введении в жидкость поверхностно активных веществ (ПАВ) значение коэффициента поверхностного натяжения
становится равным нулю. При введении в жидкость поверхностно активных веществ (ПАВ) значение коэффициента поверхностного натяжения 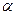 будет уменьшаться.
будет уменьшаться.
2.2 Давление под изогнутой поверхностью жидкости
Рассмотрим поверхность жидкости, опирающуюся на некоторый плоский контур, выпуклую и вогнутую поверхности (рисунок 2.2).
 |
а) б) в)
Рисунок 2.2 – Поверхность жидкости, опирающаяся на а) плоский контур, б) выпуклую поверхность, в) вогнутую поверхность
Если поверхность не плоская, то сокращение жидкости приводит к появлению дополнительного давления 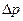 . При выпуклой поверхности выполняется условие
. При выпуклой поверхности выполняется условие 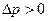 . Если поверхность вогнутая, тогда
. Если поверхность вогнутая, тогда 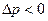 .
.
Если сферическую каплю жидкости рассечь диаметральной плоскостью на два полушария (рисунок 2.3), то оба полушария из-за поверхностного натяжения будут притягиваться друг к другу с силой, равной
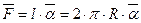 , (2.5)
, (2.5)
где 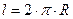 – длина окружности с радиусом
– длина окружности с радиусом 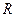 , который одновременно является радиусом сферы.
, который одновременно является радиусом сферы.
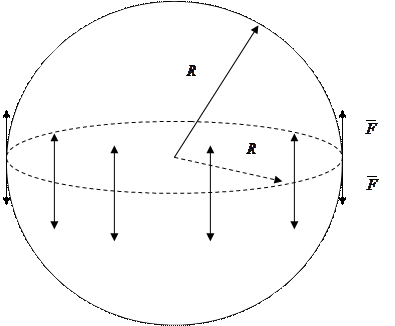 |
Рисунок 2.3 – Капля жидкости, рассечённая диаметральной плоскостью
Сила 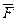 прижимает полушария друг к другу по поверхности площадью равной
прижимает полушария друг к другу по поверхности площадью равной 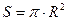 , обуславливая дополнительное давление
, обуславливая дополнительное давление
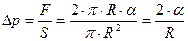 . (2.6)
. (2.6)
Кривизна сферической поверхности определяется её радиусом 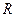 . Если уменьшить радиус, кривизна поверхности станет больше. Введём понятие «средней кривизны». В любой точке поверхности сферы кривизна может быть различной из-за искажения формы капли, поскольку форма капли неустойчива. Среднюю кривизну будем определять через кривизну нормальных сечений. Количественно кривизна оценивается с помощью величины
. Если уменьшить радиус, кривизна поверхности станет больше. Введём понятие «средней кривизны». В любой точке поверхности сферы кривизна может быть различной из-за искажения формы капли, поскольку форма капли неустойчива. Среднюю кривизну будем определять через кривизну нормальных сечений. Количественно кривизна оценивается с помощью величины 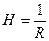 . Геометрически доказано, что
. Геометрически доказано, что
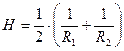 ,
,
где 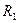 и
и  – радиусы кривизны поверхности, проведённые к двум различным точкам поверхности сферы. Если центр кривизны находится под нормальной поверхностью, то будет выполняться условие
– радиусы кривизны поверхности, проведённые к двум различным точкам поверхности сферы. Если центр кривизны находится под нормальной поверхностью, то будет выполняться условие 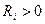 . В противном случае
. В противном случае 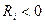 .
.
Представим себе «седло», как показано на рисунке 2.4.
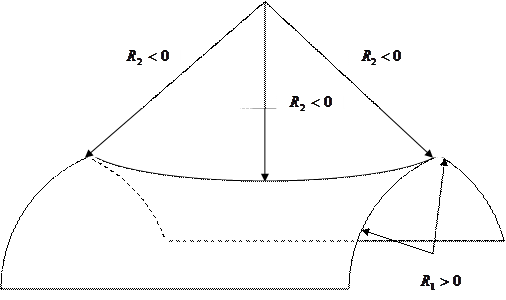 |
Рисунок 2.4 – Поверхность в виде «седла», имеющая в некоторых точках положительные или отрицательные радиусы кривизны
Для участка поверхности сферы, если выполняется условие 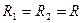 , степень кривизны рассчитывается с помощью выражения (2.7):
, степень кривизны рассчитывается с помощью выражения (2.7):
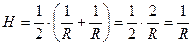 . (2.7)
. (2.7)
Тогда радиус кривизны поверхности равен 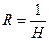 , а дополнительное давление равно
, а дополнительное давление равно
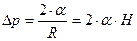 . (2.8)
. (2.8)
Если учесть среднюю кривизну, то для произвольной поверхности будет справедливо соотношение
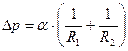 . (2.9)
. (2.9)
Выражение (2.9) является формулой Лапласа.
Добавочное давление 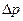 изменяет уровень жидкости в узких трубках – капиллярах, поэтому иногда оно называется капиллярным давлением. Рассмотрим два сечения кругового цилиндра: продольное и поперечное (рисунок 2.5). В продольном сечении цилиндр имеет бесконечную величину
изменяет уровень жидкости в узких трубках – капиллярах, поэтому иногда оно называется капиллярным давлением. Рассмотрим два сечения кругового цилиндра: продольное и поперечное (рисунок 2.5). В продольном сечении цилиндр имеет бесконечную величину 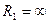 и конечную величину
и конечную величину 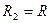 . Кривизна поверхности цилиндра
. Кривизна поверхности цилиндра 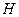 равна
равна
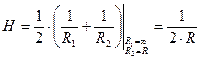 ,
,
а добавочное давление 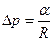 .
.
 |
а) б)
Рисунок 2.5 – Сечения кругового цилиндра: а) продольное, б) поперечное
Если в жидкости имеется пузырёк газа, то поверхность пузырька, стремясь сократиться, будет оказывать на газ дополнительное давление, которое рассчитывается с помощью выражения (2.8).
2.3 Явления на границе жидкости и твёрдого тела. Смачивание
Как и жидкости, твёрдые тела тоже обладают поверхностным натяжением. Если граничат между собой твёрдое тело, жидкость и газ, тогда суммарная потенциальная энергия их молекул будет минимальной. Условие равновесия контура «твёрдое тело – жидкость – газ», как следует из рисунка 2.6, заключается в равенстве нулю суммы проекций векторов 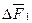 ,
, 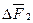 и
и 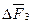 :
:
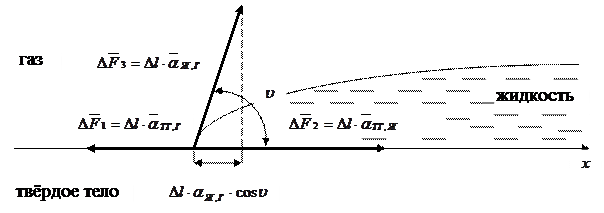 |
Рисунок 2.6 – Условие равновесия контура «твёрдое тело – жидкость – газ»
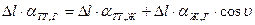 . (2.10)
. (2.10)
Из выражения (2.10) определяем величину 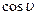 :
:
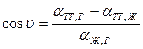 . (2.11)
. (2.11)
Поскольку для величины косинуса справедливо соотношение 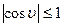 , то в окончательном виде условие равновесия контура «твёрдое тело – жидкость – газ» имеет вид:
, то в окончательном виде условие равновесия контура «твёрдое тело – жидкость – газ» имеет вид:
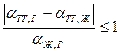 . (2.12)
. (2.12)
В выражениях (2.10 – 2.12):
- 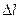 – линейный размер поверхности среды;
– линейный размер поверхности среды;
- 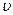 – краевой угол – угол между касательной к поверхности твёрдого тела и касательной к поверхности жидкости;
– краевой угол – угол между касательной к поверхности твёрдого тела и касательной к поверхности жидкости;
- 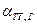 – коэффициент поверхностного натяжения контура «твёрдое тело – газ»;
– коэффициент поверхностного натяжения контура «твёрдое тело – газ»;
- 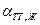 – коэффициент поверхностного натяжения контура «твёрдое тело – жидкость»;
– коэффициент поверхностного натяжения контура «твёрдое тело – жидкость»;
- 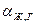 – коэффициент поверхностного натяжения контура «жидкость – газ»;
– коэффициент поверхностного натяжения контура «жидкость – газ»;
- 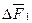 – приращение силы поверхностного натяжения контура «твёрдое тело – газ»;
– приращение силы поверхностного натяжения контура «твёрдое тело – газ»;
- 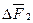 – приращение силы поверхностного натяжения контура «твёрдое тело – жидкость»;
– приращение силы поверхностного натяжения контура «твёрдое тело – жидкость»;
- 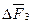 – приращение силы поверхностного натяжения контура «жидкость – газ».
– приращение силы поверхностного натяжения контура «жидкость – газ».
Условие (2.12) выполняется, если 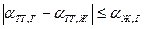 . В противном случае, когда
. В противном случае, когда 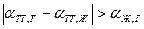 – равновесие не устанавливается. Равновесие не устанавливается в двух случаях:
– равновесие не устанавливается. Равновесие не устанавливается в двух случаях:
1. При условии, что 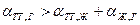 . В этом случае имеет место полное смачивание, когда величина краевого угла
. В этом случае имеет место полное смачивание, когда величина краевого угла 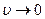 (рисунок 2.7 «а»);
(рисунок 2.7 «а»);
2. При условии, что 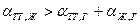 . В этом случае имеет место полное несмачивание, когда величина краевого угла
. В этом случае имеет место полное несмачивание, когда величина краевого угла 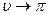 (рисунок 2.7 «б»).
(рисунок 2.7 «б»).
 |
а) б)
Рисунок 2.7 – Полное а) смачивание, б) несмачивание
Таким образом, полное смачивание – это явление замены поверхности «твёрдое тело – газ» поверхностями «твёрдое тело – жидкость» и «жидкость – газ». Полное несмачивание – это явление замены поверхности «твёрдое тело – жидкость» поверхностями «твёрдое тело – газ» и «жидкость – газ».
В том случае, когда 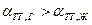 , краевой угол является острым (
, краевой угол является острым (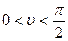 ). В этом случае имеет место частичное смачивание. Если
). В этом случае имеет место частичное смачивание. Если 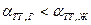 , краевой угол является тупым (
, краевой угол является тупым (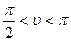 ). В этом случае имеет место частичное несмачивание.
). В этом случае имеет место частичное несмачивание.
Поскольку существует краевой угол 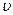 , то поверхность жидкости у стенок сосуда искривляется. В капилляре, представляющим собой тонкую трубку, искривляется вся поверхность жидкости. При этом:
, то поверхность жидкости у стенок сосуда искривляется. В капилляре, представляющим собой тонкую трубку, искривляется вся поверхность жидкости. При этом:
- если жидкость смачивает твёрдое тело (стенки капилляра), то форма поверхности жидкости будет вогнутой;
- если жидкость стенки капилляра не смачивает, то форма поверхности жидкости будет выпуклой.
Такие изогнутости поверхностей называются менисками.
Если жидкость смачивает стенки капилляра, то уровень жидкости в нём будет выше. В противном случае – ниже. Изменение высоты уровня жидкости в капилляре называется капиллярностью. Между жидкостью в капилляре и широком сосуде устанавливается такая разность уровней 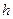 , чтобы гидростатическое давление
, чтобы гидростатическое давление 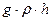 уравновешивало капиллярное давление
уравновешивало капиллярное давление 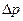 :
:
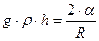 , (2.13)
, (2.13)
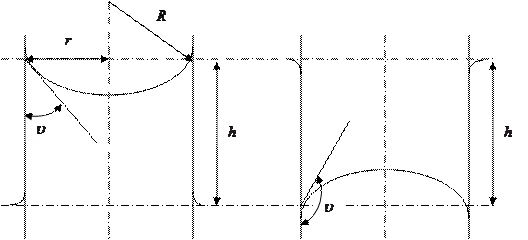
где 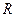 – радиус кривизны мениска (рисунок 2.8), а
– радиус кривизны мениска (рисунок 2.8), а 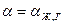 .
.
 |
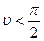 ,
, 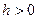
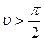 ,
, 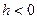
а) б)
Рисунок 2.8 – Изменение уровня жидкости в капилляре
Поскольку в выражении (2.13) величина 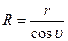 , то данное выражение запишется в виде
, то данное выражение запишется в виде
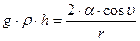 , (2.14)
, (2.14)
где 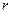 – радиус поперечного сечения капилляра.
– радиус поперечного сечения капилляра.
Из выражения (2.14) определяется разность уровней
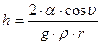 . (2.15)
. (2.15)
Как следует из рисунка 2.8:
при 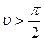 косинус угла
косинус угла 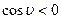 , разность уровней
, разность уровней 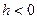 , следовательно жидкость не смачивает капилляр;
, следовательно жидкость не смачивает капилляр;
при 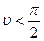 косинус угла
косинус угла 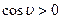 , разность уровней
, разность уровней 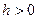 , следовательно жидкость смачивает капилляр.
, следовательно жидкость смачивает капилляр.
Для мениска произвольной формы равновесие соответствует минимальному значению потенциальной энергии системы «жидкость – капилляр». Определим зависимость приращения потенциальной энергии 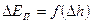 от разности уровней.
от разности уровней.
При увеличении значения 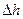 площадь поверхности соприкосновения жидкости с капилляром возрастает на величину
площадь поверхности соприкосновения жидкости с капилляром возрастает на величину 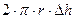 , а приращение потенциальной энергии – на величину
, а приращение потенциальной энергии – на величину 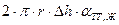 . Одновременно при увеличении значения
. Одновременно при увеличении значения 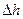 площадь поверхности соприкосновения капилляра с газом уменьшается, следовательно, уменьшается приращение потенциальной энергии на величину
площадь поверхности соприкосновения капилляра с газом уменьшается, следовательно, уменьшается приращение потенциальной энергии на величину 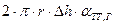 .
.
Как следует из рисунка 2.9, потенциальная энергия жидкости в поле земного тяготения получает приращение, равное весу заштрихованного объёма жидкости, умноженного на величину 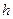 :
:
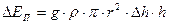 . (2.16)
. (2.16)
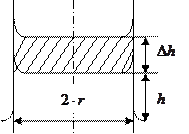 |
Рисунок 2.9 – Соприкосновение капилляра с жидкостью и газом
При изменении на одну единицу уровня жидкости, получаем:
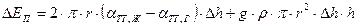 .
.
Дифференцируя полученное выражение по переменной 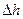 , приравняем его к нулю:
, приравняем его к нулю:
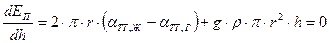 .
.
Тогда:
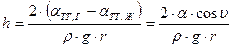 , (2.17)
, (2.17)
где косинус краевого угла 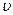 определяется с помощью выражения (2.11).
определяется с помощью выражения (2.11).
Если вместе сложить две отшлифованные смоченные жидкостью пластинки (рисунок 2.10), то между ними возникает сила сцепления, т.к. поверхность жидкости в зазоре между пластинами сильно искривлена.
 |
Рисунок 2.10 – Отшлифованные смоченные жидкостью пластинки
Поэтому давление 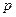 внутри жидкости будет меньше атмосферного на величину
внутри жидкости будет меньше атмосферного на величину
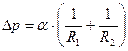 .
.
При полном смачивании, когда 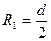 , а
, а 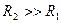 разница давлений приблизительно будет равна значению
разница давлений приблизительно будет равна значению 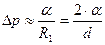 .
.
Если смоченная поверхность имеет площадь 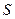 , то сила, с которой пластинки будут прижиматься друг к другу, определяется по формуле (2.18):
, то сила, с которой пластинки будут прижиматься друг к другу, определяется по формуле (2.18):
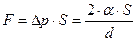 . (2.18)
. (2.18)
 2015-03-27
2015-03-27 2055
2055
