2015-06-05
5185
Еще в XVII в. было обнаружено, что при погружении в жидкость капилляра (узкой трубки) уровень жидкости, смачивающей стенки капилляра, выше, чем ее аналогичный уровень в широком сосуде. Причем уровень жидкости в капилляре тем выше, чем меньше радиус капилляра (h 2 > h 1).
При смачивании (θ < 90°) образуется вогнутый мениск, жидкость в капилляре поднимается. Это явление называется капиллярным поднятием жидкости (рис. 2.9). Жидкость поднимается тем выше, чем меньше радиус капилляра (h 2 > h 1).
Например, поднятие уровня воды в стеклянном капилляре.
Несмачивание (θ > 90°), образуется выпуклый мениск, уровень жидкости в капилляре опускается. Жидкость опускается тем ниже, чем меньше радиус капилляра (h 2 > h 1). Это явление называется капиллярной депрессией жидкости (рис. 2.10).
Например, опускание уровня ртути в стеклянном капилляре.
 |  |
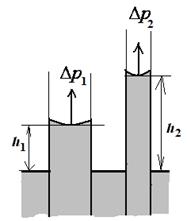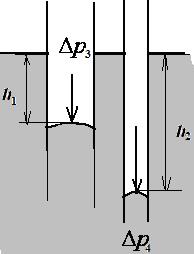| Рис. 2.9. Капиллярной поднятие жидкости | Рис. 2.10. Капиллярная депрессия жидкости |
Таким образом, существует однозначное соответствие между знаком кривизны капиллярного мениска, радиусом капилляра и высотой поднятия (опускания) уровня жидкости в капилляре.
В случае смачивания жидкостью стенок капилляра, поверхность жидкости имеет отрицательную кривизну, поэтому дополнительное давление Лапласа стремиться растянуть жидкость (давление направлено к центру кривизны) и поднимает ее в капилляре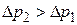 
.
В случае несмачивания жидкостью стенок капилляра, кривизна поверхности жидкости будет положительной, дополнительное давление Лапласа будет направлено внутрь жидкости (жидкость будет сжиматься), в результате чего жидкость в капилляре опускается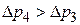 
.
Установим количественную зависимость высоты поднятия уровня жидкости в капилляре h от радиуса кривизны мениска r, радиуса капилляра R, краевого угла смачивания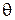 
и поверхностного натяжения искривленной поверхности 
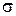, разделяющей жидкую и газообразную фазы.
При равновесии избыточное лапласовское давление равно гидростатическому давлению столба жидкости высотой h:
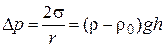, (2.26)
отсюда
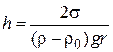, (2.27)
где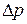 
– избыточное внутримолекулярное давление; 
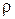– плотность жидкости; 
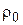– плотность газа; g – ускорение свободного падания, равное 9,81 м/с2; r – радиус мениска.
Из рис. 2.11 видно, что радиус мениска r связан с радиусом капилляра R через краевой угол смачивания :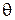
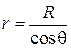. (2.28)
Тогда высоту капиллярного поднятия жидкости можно представить:
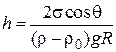. (2.29)
Полученное выражение (2.29) носит название уравнения Жюрена.
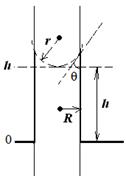
Рис. 2.11. Равновесное состояние
капиллярного поднятия жидкости
Так как плотность жидкости много больше плотности равновесного с ней пара 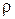>> 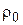, то уравнение Жюрена имеет вид:
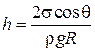. (2.30)
