Дифференцируемость функции нескольких переменных. Дифференциал, его свойства. Применение дифференциала к приближенным вычислениям. Дифференцирование сложных функций. Инвариантность формы дифференциала.
При исследовании вопросов, связанных с дифференцируемостью, ограничимся случаем функции трех переменных, поскольку все доказательства для большего количества переменных проводятся так же.
Определение 2.1. Полным приращением функции u = f(x, y, z) называется
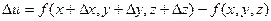 (2.1)
(2.1)
Теорема 2.1. Если частные производные 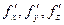 существуют в точке (х0, у0, z0) и в некоторой ее окрестности и непрерывны в точке (x0, y0, z0), то
существуют в точке (х0, у0, z0) и в некоторой ее окрестности и непрерывны в точке (x0, y0, z0), то
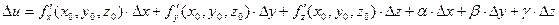 , (2.2)
, (2.2)
где α, β, γ – бесконечно малые, зависящие от Δ х, Δ у, Δ z.
Доказательство.
Представим полное приращение Δ u в виде:
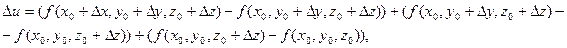 ,
,
где каждая разность представляет собой частное приращение функции только по одной из переменных. Из условия теоремы следует, что к этим разностям можно применить теорему Лагранжа. При этом получим:
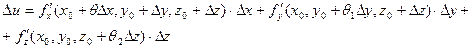 .
.
Так как по условию теоремы частные производные непрерывны в точке (х0, у0, z0), можно представить их в виде:
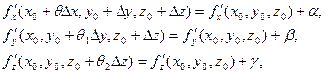
где 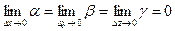 . Теорема доказана.
. Теорема доказана.
Можно показать, что 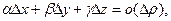 где
где 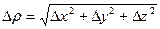 . Действительно, α, β и γ – бесконечно малые при ρ→0, а
. Действительно, α, β и γ – бесконечно малые при ρ→0, а 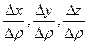 - ограниченные (т.к. их модули не превышают 1).
- ограниченные (т.к. их модули не превышают 1).
Тогда приращение функции, удовлетворяющей условиям теоремы 2.1, можно представить в виде: 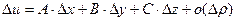 , (2.3)
, (2.3)
где 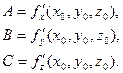 (2.4)
(2.4)
Определение 2.2. Если приращение функции u = f (x, y, z) в точке (x0, y0, z0) можно представить в виде (2.3), (2.4), то функция называется дифференцируемой в этой точке, а выражение 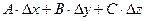 - главной линейной частью приращения или полным дифференциалом рассматриваемой функции.
- главной линейной частью приращения или полным дифференциалом рассматриваемой функции.
Обозначения: du, df (x0, y0, z0).
Так же, как в случае функции одной переменной, дифференциалами независимых переменных считаются их произвольные приращения, поэтому

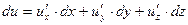 (2.5)
(2.5)
Замечание 1. Итак, утверждение «функция дифференцируема» не равнозначно утверждению «функция имеет частные производные» - для дифференцируемости требуется еще и непрерывность этих производных в рассматриваемой точке.
Замечание 2. Если в формуле (2.5) считать 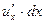 ,
, 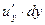 и
и 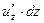 частными дифференциалами данной функции (как функции одного из аргументов), то можно сказать, что полный дифференциал равен сумме частных дифференциалов.
частными дифференциалами данной функции (как функции одного из аргументов), то можно сказать, что полный дифференциал равен сумме частных дифференциалов.
Применение дифференциала к приближенным вычислениям.
По аналогии с линеаризацией функции одной переменной можно при приближенном вычислении значений функции нескольких переменных, дифференцируемой в некоторой точке, заменять ее приращение дифференциалом. Таким образом, можно находить приближенное значение функции нескольких (например, двух) переменных по формуле:
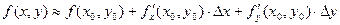 , (2.6)
, (2.6)
где 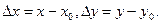
Пример.
Вычислить приближенное значение 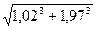 .
.
Рассмотрим функцию 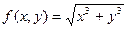 и выберем х0 = 1, у0 = 2. Тогда Δ х = 1,02 – 1 = 0,02; Δ у = 1,97 – 2 = -0,03. Найдем
и выберем х0 = 1, у0 = 2. Тогда Δ х = 1,02 – 1 = 0,02; Δ у = 1,97 – 2 = -0,03. Найдем 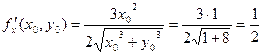 ,
,
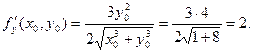 Следовательно, учитывая, что f ( 1, 2) = 3, получим:
Следовательно, учитывая, что f ( 1, 2) = 3, получим:
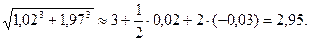
 2015-03-27
2015-03-27 2482
2482
