2015-03-27
595
Частные производные функции z = f (x,y) являются, в свою очередь, функциями переменных х и у. Следовательно, можно найти их частные производные по этим переменным. Обозначим их так:
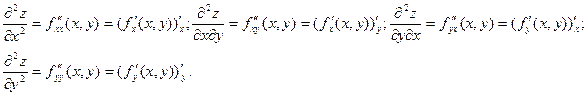
Таким образом, получены четыре частные производные 2-го порядка. Каждую из них можно вновь продифференцировать по х и по у и получить восемь частных производных 3-го порядка и т.д. Определим производные высших порядков так:
Определение 3.2. Частной производной n -го порядка функции нескольких переменных называется первая производная от производной (n – 1)-го порядка.
Частные производные обладают важным свойством: результат дифференцирования не зависит от порядка дифференцирования (например,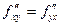 
). Докажем это утверждение.
Теорема 3.3. Если функция z = f (x,y) и ее частные производные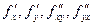 
определены и непрерывны в точке М (х, у) и в некоторой ее окрестности, то в этой точке
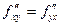(3.3)
Доказательство.
Рассмотрим выражение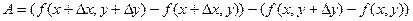 
и введем вспомогательную функцию 
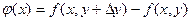. Тогда
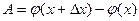. Из условия теоремы следует, что 
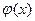дифференцируема на отрезке [ x, x+ Δ x ], поэтому к ней можно применить теорему Лагранжа: 
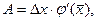где
|
|
|
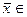[ x, x+ Δ x ]. Но 
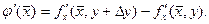Так как в окрестности точки М определена 
, 
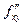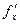дифференцируема на отрезке [ y, y + Δ y ], поэтому к полученной разности вновь можно применить теорему Лагранжа: 
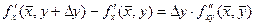, где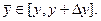 
Тогда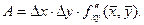 
Изменим порядок слагаемых в выражении для А:
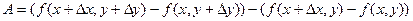и введем другую вспомогательную функцию 
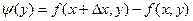, тогда 
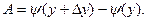Проведя те же преобразования, что и для 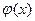, получим, что 
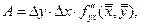где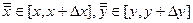 
. Следовательно,
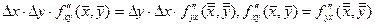. В силу непрерывност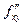и и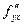 
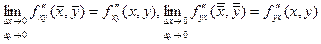. Поэтому, переходя к пределу при 
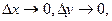получаем, что 
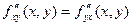, что и требовалось доказать.
Следствие. Указанное свойство справедливо для производных любого порядка и для функций от любого числа переменных.
Дифференциалы высших порядков.
Определение 3.2. Дифференциалом второго порядка функции u = f (x, y, z) называется
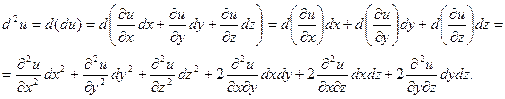
Аналогично можно определить дифференциалы 3-го и более высоких порядков:
Определение 3.3. Дифференциалом порядка k называется полный дифференциал от дифференциала порядка (k – 1): d k u = d (d k- 1 u).
Свойства дифференциалов высших порядков.
- k -й дифференциал является однородным целым многочленом степени k относительно дифференциалов независимых переменных, коэффициентами при которых служат частные производные k -го порядка, умноженные на целочисленные постоянные (такие же, как при обычном возведении в степень):
.
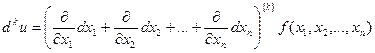- Дифференциалы порядка выше первого не инвариантны относительно выбора переменных.
Лекция 4.
Касательная плоскость и нормаль к поверхности. Геометрический смысл дифференциала. Формула Тейлора для функции нескольких переменных. Производная функции по направлению. Градиент и его свойства.
|
|
|
Пусть функция z = f (x, y) является дифференцируемой в окрестности точки М (х0, у0). Тогда ее частные производные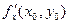 
и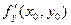 
являются угловыми коэффициентами касательных к линиям пересечения поверхности z = f (x, y) с плоскостями у = у0 и х = х0, которые будут касательными и к самой поверхности z = f (x, y). Составим уравнение плоскости, проходящей через эти прямые. Направляющие векторы касательных имеют вид {1; 0; 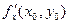} и {0; 1; 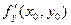}, поэтому нормаль к плоскости можно представить в виде их векторного произведения: n = {- 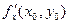,- , 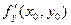1}. Следовательно, уравнение плоскости можно записать так:
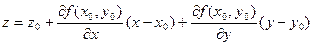, (4.1)
где z0 =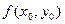 
.
Определение 4.1. Плоскость, определяемая уравнением (4.1), называется касательной плоскостью к графику функции z = f (x, y) в точке с координатами (х0, у0, z0).
Из формулы (2.3) для случая двух переменных следует, что приращение функции f в окрестности точки М можно представить в виде:
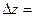
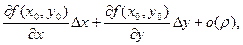или
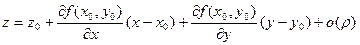(4.2)
Следовательно, разность между аппликатами графика функции и касательной плоскости является бесконечно малой более высокого порядка, чем ρ, при ρ→ 0.
При этом дифференциал функции f имеет вид:
,
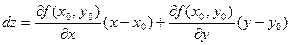что соответствует приращению аппликаты касательной плоскости к графику функции. В этом состоит геометрический смысл дифференциала.
Определение 4.2. Ненулевой вектор, перпендикулярный касательной плоскости в точке М (х0, у0) поверхности z = f (x, y), называется нормалью к поверхности в этой точке.
В качестве нормали к рассматриваемой поверхности удобно принять вектор -- n = { 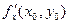, ,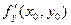-1}.
z
 |
z = f (x,y)
M0 (x0, y0, z0)
n
 |
y
M (x0, y0)
x
Пример.
Составим уравнение касательной плоскости к поверхности z = xy в точке М (1; 1). При х0 = у0 = 1 z0 = 1;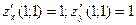 
. Следовательно, касательная плоскость задается уравнением: z = 1 + (x – 1) + (y – 1), или x + y – z – 1 = 0. При этом вектор нормали в данной точке поверхности имеет вид: n = {1; 1; -1}.
Найдем приращение аппликат графика функции и касательной плоскости при переходе от точки М к точке N (1,01; 1,01).
Δ z = 1,01² - 1 = 0,0201; Δ z кас = (1,01 + 1,01 – 1) – (1 + 1 – 1) = 0,02. Следовательно,
dz = Δ z кас = 0,02. При этом Δ z – dz = 0,0001.
