2015-03-27
1252
1. Кривые, среднее за период значение которых равно нулю, не содержат постоянной составляющей (нулевой гармоники).
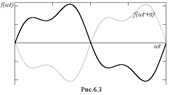2. Если функция удовлетворяет условию f(ωt)=-f(ωt+π), то она называется симметричной относительно оси абсцисс. Этот вид симметрии легко определить по виду кривой: если сместить её на полпериода по оси абсцисс, зеркально отобразить и при этом она сольётся с исходной кривой (рис.6.3), то симметрия имеется. При разложении такой кривой в ряд Фурье в последнем отсутствует постоянная составляющая и все четные гармоники, поскольку они не удовлетворяют условию f(ωt)=-f(ωt+π). Следовательно, для таких кривых
f(ωt)=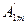 
sin(ωt+ψ 1 )+ 
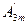sin(3ωt+ψ 3 )+ 
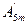sin(5ωt +ψ 5 )+···.
3. Если функция удовлетворяет условию f(ωt)=f(-ωt), то она называется симметричной относительно оси ординат (четной). Этот вид симметрии легко определить по виду кривой: если кривую, лежащую левее оси ординат, зеркально отобразить и она сольется с исходной кривой, то симметрия имеется (рис.6.4). При разложении такой кривой в ряд Фурье в последнем будут отсутствовать синусные составляющие всех гармоник (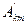
= 0), поскольку они не удовлетворяют условию f(ωt)=f(-ωt). Следовательно, для таких кривых
|
|
|
f(ωt)=Ао+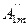 
cosωt+ 
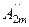cos2ωt+ 
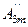cos3ωt+···.
4. Если функция удовлетворяет условию f(ωt)=-f(-ωt), то она называется симметричной относительно начала координат (нечетной). Наличие данного вида симметрии легко определить по виду кривой: если кривую, лежащую левее оси ординат развернуть относительно точки начала координат и она сольется с исходной кривой, то симметрия имеется (рис.6.5). При разложении такой кривой в ряд Фурье в последнем будут отсутствовать косинусные составляющие всех гармоник (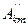
= 0), поскольку они не удовлетворяют условию f(ωt)=-f(-ωt). Следовательно, для таких кривых
f(ωt)=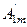 
sinωt+ 
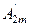sin2ωt+ 
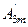sin3ωt+···.
При наличии какой-либо симметрии в формулах для 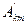и 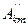можно брать интеграл за полпериода, но результат удваивать, т.е. пользоваться выражениями
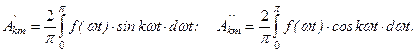
В кривых бывают и несколько видов симметрии одновременно. Для облегчения вопроса о гармонических составляющих в этом случае заполним таблицу
| Вид симметрии | Аналитическое выражение | А о |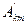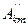
|
|
| 1. Оси абсцисс | f(ωt)=-f(ωt+π) | - | Только нечетные | |
| 2. Оси ординат | f(ωt)=f(-ωt) | + | - | + |
| 3. Начала координат | f(ωt)=-f(-ωt) | - | + | - |
| 4. Оси абсцисс и оси ординат | f(ωt)=-f(ωt+π)=f(-ωt) | - | - | Нечетные |
| 5. Оси абсцисс и начала координат | f(ωt)=-f(ωt+π)=-f(-ωt) | - | Нечетные | - |
Раскладывая кривую в ряд Фурье, следует предварительно выяснить, не обладает ли она каким-либо видом симметрии, наличие которой позволяет заранее предсказать, какие гармоники будут в ряде Фурье и не выполнять лишней работы.
|
|
|
