Представление произвольного сигнала в виде суммы элементарных колебаний. Обобщенный ряд Фурье

В 1822 году французский математик Жан Батист Жозеф Фурье (1768-1830) в своей работе "Аналитическая теория тепла" сформулировал положение о том, что любая непрерывная функция, повторяющаяся на интервале Т, может быть представлена суммой основной синусоидальной компоненты и серии гармонических составляющих более высокого порядка с частотами, кратными основной частоте.

Гармонический анализ представляет собой процесс расчета значений амплитуд и фаз основной частоты и гармоник более высокого порядка периодической кривой. Результирующий ряд известен как ряд Фурье и представляет собой соотношение между функцией во временной области и соответствующей функции в области частот.

С помощью обобщенного ряда Фурье можно показать пригодность различного класса функций, по которым возможно разложение сигналов.

Бесконечная система действительных функций

j₀(x),j₁(x),j₂(x)..., j _n (x)... (3.1)

называется ортогональной на отрезке [ a; b ], если:

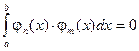при n ¹ m (3.2)

При этом предполагается, что никакая из функций j _n (x) не равна тождественно нулю, т.е.:

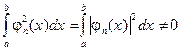(3.3)

Условие (3.2) выражает попарную орто­гональность функций системы (3.1).

Величину

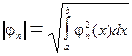(3.4)

называют нормой функции j _n (x).

Функция j _n (x), для которой выполняется условие

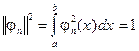(3.5)

называется нормированной функцией, а система нормированных функций (3.1), в которой каждые две различные функции взаимно ортогональны, называется ортонормированной системой.

Известно, что если функции {j _n (x)} непрерывны, то произвольная кусочно-непрерывная функция f (x), для которой выполняется условие:

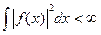(3.6)

то есть f (x) - ограниченная, абсолютно интегрируемая функция, может быть представлена в виде суммы ряда:

f (x) = C ₀j₀(x)+ C ₁j₁(x)+ C ₂j₂(x)+...+ C_n j _n (x)...(3.7)

Коэффициенты С_n суммы (3.7) можно определить, если умножить обе части (3.7) на j _n (x) и проинтегрировать в обла­с­ти ортогональности функций j _n (x) [ a; b ]. Все слагаемые вида

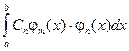при n ¹ m

обращаются в нуль в силу ортогональности функций j _n (x) и j _m (x), а в правой части остается одно слагаемое:

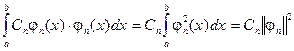
отсюда:

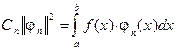, или, по другому:

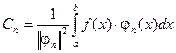(3.8)

Ряд (3.7), в котором коэффициенты С_n определены по формуле (3.8), называется обобщенным рядом Фурье по данной системе {j _n (x)}.

Совокупность коэффициентов С_n называется спектром сигнала f (x) в ортогональной системе {j _n (x)} и полностью определяет этот сигнал.

Обобщенный ряд Фурье обладает важным свойством:

- при заданной системе функций {j _n (x)} и конечном числе N членов суммы ряда (3.7) он обеспечивает наилучшую аппроксимацию (в смысле минимума средне­квадратической ошибки) заданной функции f (x).

Это значит, что среднеквадратическая ошибка достигает минимума, когда коэффициенты ряда (3.7) вычислены по формуле (3.8), то есть явля­ются коэффициентами ряда Фурье.

Среднеквадратическая ошибка имеет
следующий вид:

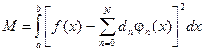(3.9)

Действительно, подставляя d_n = с_n + e_n и
использовав равенства (3.4) и (3.8), получим:

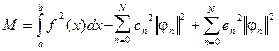
Отсюда следует, что ошибка М достигает
минимума при e_n = 0, то есть при d_n = с_n. Тогда ошибка для конечного числа членов ряда (3.7) принимает вид:

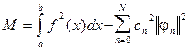(3.10)

Замечая, что первая часть разности (3.10) есть квадрат нормы функции f (x), а min (М) неотрицателен, на основании равенства (3.10) можно записать:

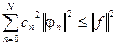(3.11)

Это основное неравенство, называемое
неравенством Бесселя, справедливо для любой ортогональной системы и является весьма эффективным при оценке приближения по мере постепенного увеличе­ния числа членов ряда Фурье.

Ортогональная система называется полной, если увеличением числа членов в ряде среднеквадратическую ошибку М можно
сделать сколь угодно малой.

Условие полноты системы можно выразить следующим образом:

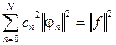(3.12)

При выполнении (3.12) считают, что ряд (3.7) сходится в среднем, то есть:

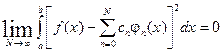(3.13)

Из этого, однако, еще не следует, что 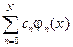сходится к f (x) при любых значениях x, то есть что:

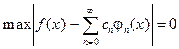
В отдельных точ­ках на оси Х ряд (3.7) может отличаться от f (x), хотя равенство (3.13) имеет место (когда f (x) терпит разрыв 1 ^го рода в конечном числе точек х _{0 n} ). В част­ности­, если функция f (x) имеет разрывы так, что в некоторой точке x₀:

f (x ₀ - 0) ¹ f (x ₀ + 0),

то тогда ряд Фурье в этой точке сходится к среднеарифметическому значению:

½[ f (x ₀ - 0) + f (x ₀ + 0)].

Равенство нулю среднеквадратической погрешности разложения при этом возможно лишь потому, что мы имеем конеч­ную погрешность, но на бесконечно малом промежутке изменения аргумента.

Для системы функций {j _n (x)}, принимающих комплексные значения, приведенные выше условия и определения обобщаются следующим образом:

- условие ортогональности:

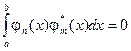(3.14)

- квадрат нормы функции:

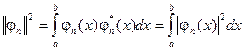(3.15)

- коэффициенты Фурье:

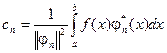(3.16)

Здесь j ^* (x) - функция, комплексно сопря­женная c j(x).

Наиболее часто приходится обрабатывать сигналы, представляющие собой функции времени t, поэтому для таких сигналов s (t) выражение (3.7) будем записывать в виде:

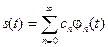(3.17)

Понятно, что этот ряд справедлив для функций аргумента, имеющего любую природу. В новых обозначениях квадрат нормы функции s (t) по аналогии с (3.4) будет иметь вид:

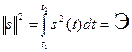(3.18)

где Э - энергия сигнала s (t) на интервале [ t ₁, t ₂].

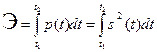
(интеграл от мгновенной мощности p (t) на интервале [ t ₁, t ₂]). Или, в соответствии с (3.12), энергия сигнала

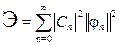(3.19)

При использовании ортонормированной
системы функций {j _n (t)}:

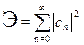(3.20)

При этом имеется в виду, что промежуток времени (t ₂- t ₁), в котором определяется энергия Э, является интервалом ортогональности для системы функций {j _n (t)}.

Очевидно, что средняя за время (t ₂ -t ₁) мощность сигнала

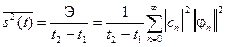(3.21)

Выбор наиболее рациональной ортогональной системы функций зависит от цели, преследуемой при разложении сложной функции в ряд. Среди задач, требующих разложения сигнала, наиболее важными представляются:

1) Точное разложение на простейшие ортогональные функции;

2) Аппроксимация сигналов, процессов или характеристик по возможности минимальным числом членов ряда (при задан­ной допустимой погрешности).

При первой постановке задачи среди всех возможных видов базовых функций, несомненно, самыми распространенными являются гармонические. Это объясняется тем, что только гармонические (синусои­да­ль­ные) сигналы являются единственными функциями времени, сохраняющими свою форму при прохождении через любую линейную цепь (с постоянными параметрами): может измениться амплитуда и/или фаза, но форма и частота синусоидального сигнала не изменяются. Таким образом, гармонические функции являются собственными функциями для линейных преобразований. Кроме того, такое разложение позволяет использовать символический метод анализа передачи гармонического колебания через линейную цепь.

При второй постановке задачи - приближенном разложении функций - применяются разнообразные ортогональные системы функций: полиномы Чебышева, Эрмита, Лагерра, Лежандра, кусочно - постоянные функции Уолша, Хаара и многие другие.