ВЫСШАЯ МАТЕМАТИКА
БОГДАНОВ А. Е.
(ЛЕКЦИИ)
(МК 6)
(Ряды Фурье. Элементы математической физики. Элементы теории функции комплексного переменного.Операционное исчисление)
Ряды Фурье используются для описания периодических процессов, решения дифференциальных уравнений, приближения периодических и непериодических функций. Во всех этих случаях функцию, описывающую периодический процесс, представляют как сумму конечного или бесконечного числа простых периодических функций
А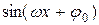 ,
,
где А, ω, φ 0 – постоянные. Эти функции называются гармониками, т.к. они описывают простейшее колебательное движение, называемое гармоническим. Постоянная А > 0 называется амплитудой колебания, ω – частота колебания, 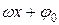 − фазой колебания, φ 0 – начальной фазой.
− фазой колебания, φ 0 – начальной фазой.
Используя формулы сложения тригонометрических функций, простую гармонику можно представить в виде
А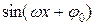 = а
= а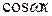 +
+ 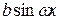 ,
,
где а = А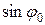 ; b = А
; b = А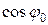 .
.
Часто сложные периодические процессы, например волновые, описываются дифференциальными уравнениями. Решения таких уравнений получаются в виде конечного или бесконечного числа простых гармоник, т.е. функций вида
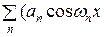 +
+ 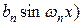 .
.
Итак, ряды Фурье связаны с периодическими функциями.
Основные понятия
Функциональный ряд вида
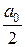 + а 1
+ а 1 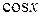 + b 1
+ b 1 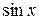 + а 2
+ а 2 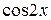 + b 2
+ b 2 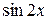 + … =
+ … = 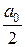 +
+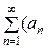
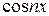 +
+ 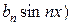 . (1)
. (1)
называется тригонометрическим рядом. Постоянные числа а 0, ап и bп (п = 1, 2, …) называются коэффициентами тригонометрического ряда.
Если (1) сходится, то его сумма S (x)есть периодическая функция f (x) с периодом 2 π (функции 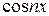 и
и 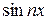 имеют период 2 π), т.е.
имеют период 2 π), т.е.
S (x) = f (x) = f (x + 2 π).
Пусть функция f (x) с периодом 2 π представляется тригонометрическим рядом, сходящимся к данной функции на отрезке [− π, π ], т.е. является суммой этого ряда:
f (x) = 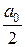 +
+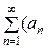
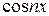 +
+ 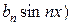 . (2)
. (2)
Пусть ряд
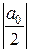 +| а 1|+| b 1|+| а 2|+| b 2|+…+| аn |+| bn |+… (3)
+| а 1|+| b 1|+| а 2|+| b 2|+…+| аn |+| bn |+… (3)
абсолютно сходится. Тогда (1) мажорируем и его можно интегрировать в промежутке от − π до π.
Проинтегрируем обе части (2) в пределах от − π до π:
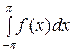 =
=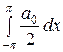 +
+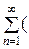
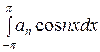 +
+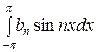 ) = πа 0, т.к.
) = πа 0, т.к.
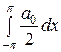 = πа 0,
= πа 0, 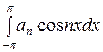 = 0,
= 0, 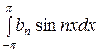 = 0.
= 0.
Таким образом,
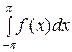 = πа 0.
= πа 0.
Отсюда следует
а 0 = 
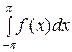 . (4)
. (4)
Известно, что если k и п целые числа, то
при k 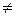 n:
n:
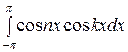 = 0,
= 0, 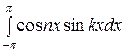 = 0,
= 0, 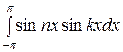 = 0; (*)
= 0; (*)
при k = n:
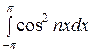 = π,
= π, 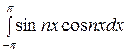 = 0,
= 0, 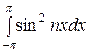 = π. (**)
= π. (**)
Пусть п 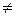 0. Умножим (2) на
0. Умножим (2) на 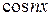 :
:
f (x) 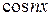 =
= 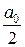
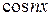 +
+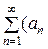
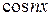
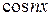 +
+ 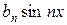
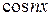 ). (
). ( )
)
В правой части ( ) ряд мажорируем, т.к. его члены не превосходят по абсолютной величине членов сходящегося ряда (3). Поэтому (
) ряд мажорируем, т.к. его члены не превосходят по абсолютной величине членов сходящегося ряда (3). Поэтому ( ) можно интегрировать на любом отрезке:
) можно интегрировать на любом отрезке:
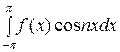 =
= 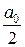
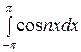 +
+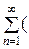
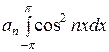 +
+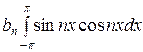 ).
).
Учитывая (*) и (**), получим
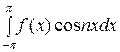 =
= 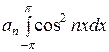 = πап,
= πап,
откуда
ап = 
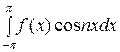 . (5)
. (5)
Умножая (2) на 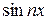 и интегрируя от − π до π, получим
и интегрируя от − π до π, получим
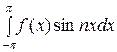 =
= 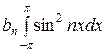 = πbп,
= πbп,
откуда
bп = 
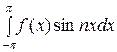 . (6)
. (6)
Коэффициенты, определенные по (4) – (6), называются коэффициентами Фурье функции f (x), а тригонометрический ряд (1) с такими коэффициентами называется рядом Фурье функции f (x).
Функция f (x) называется кусочно непрерывной на отрезке [ a, b ], если она непрерывна на этом отрезке, за исключением, быть может, конечного числа точек, где она имеет разрывы 1-го рода.
Итак, если f (x) – кусочно непрерывная функция, то в любой точке разрыва х 0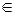 [ a, b ] существуют односторонние пределы
[ a, b ] существуют односторонние пределы
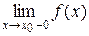 = f (x 0 − 0) и
= f (x 0 − 0) и 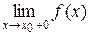 = f (x 0 + 0).
= f (x 0 + 0).
Теорема. Если периодическая функция f (x) с периодом 2 π кусочно непрерывная и ограниченная на отрезке [− π, π ] (условия Дирихле), то ряд Фурье, построенный для этой функции, сходится во всех точках. Сумма полученного ряда S (x) равна значению функции f (x) в точках непрерывности функции. В точках разрыва функции f (x) сумма ряда равняется среднему арифметическому пределов функции f (x) справа и слева, т.е., если х = х 0 – точка разрыва функции f (x), то
S (x 0) = 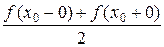 .
.
Пример (*). Периодическая функция с периодом 2 π определена следующим образом: f (x) = x, − π < x ≤ π. Разложить функцию в ряд Фурье.
□
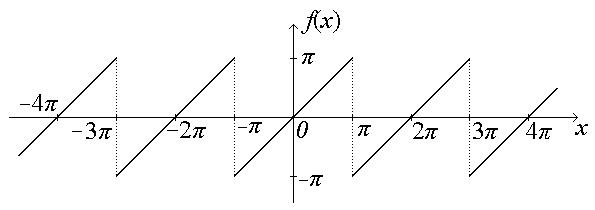
Разложение функции 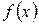 с периодом 2 π в ряд Фурье имеет вид:
с периодом 2 π в ряд Фурье имеет вид:
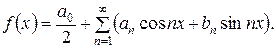
Найдем коэффициенты Фурье:
а 0 = 
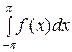 =
= 
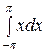 =
= 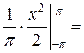
 (
(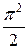 −
− 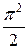 ) = 0;
) = 0;
ап = 
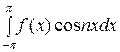 =
= 
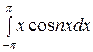 =
= 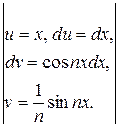 =
=  (
(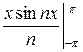 −
−
− 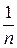
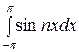 ) =
) = 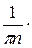
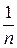
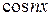
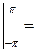
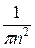 (
(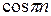 −
− 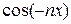 ) = 0;
) = 0;
bп = 
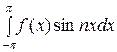 =
= 
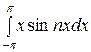 =
= 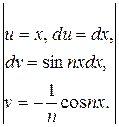 =
=  (
(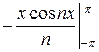 +
+
+ 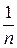
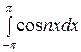 ) =
) =  (
(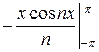 +
+ 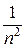
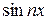
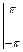 ) =
) = 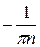 х
х 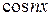
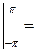
=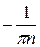 (π
(π 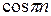 + π
+ π 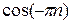 )=
)=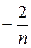
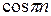 =
= 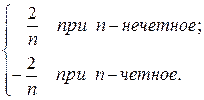 = (−1) п +1
= (−1) п +1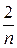 .
.
Тогда разложение будет иметь вид
х = 2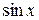 −
− 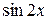 +
+ 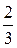
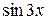 −
− 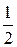
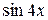 + … =
+ … = 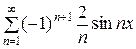 .
.
Это равенство справедливо во всех точках, кроме точек разрыва, т.е. кроме точек х 0 = ± π, ±3 π, ±5 π, … В каждой точке разрыва сумма ряда равна среднему арифметическому ее пределов справа и слева, т.е.
S (x 0)=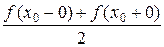 =
=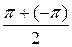 =0.
=0.
■
Замечание о разложении периодической функции в ряд Фурье
Интеграл от периодической функции  по любому отрезку, длина которого равна периоду, имеет всегда одно и то же значение.
по любому отрезку, длина которого равна периоду, имеет всегда одно и то же значение.
Этот факт легко иллюстрируется геометрически:
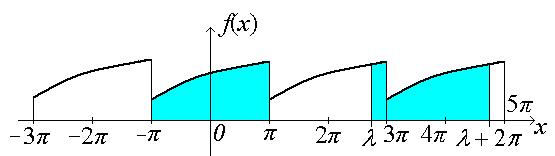
Площади, заштрихованные на рисунке, равны между собой. Таким образом, при вычислении коэффициентов Фурье можно заменить отрезок интегрирования [− π, π ] отрезком интегрирования [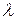 ,
, 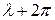 ], т.е.
], т.е.
а 0=
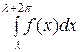 , ап =
, ап =
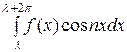 , bп =
, bп = 
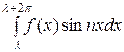 ,
,
где 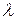 − любое число.
− любое число.
Пример. Пусть требуется разложить в ряд Фурье функцию 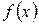 с периодом
с периодом 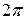 , которая на промежутке 0 < x ≤
, которая на промежутке 0 < x ≤ 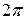 задана равенством
задана равенством 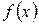 = х.
= х.
□
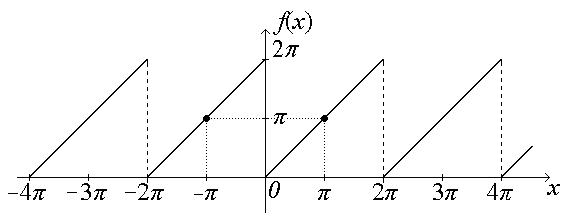
Разложение функции 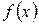 с периодом 2 π в ряд Фурье имеет вид:
с периодом 2 π в ряд Фурье имеет вид:
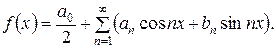
Заданная функция на промежутке 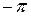 < x ≤
< x ≤ 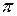 задается двумя функциями:
задается двумя функциями:
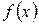 =
= 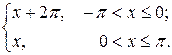
Поэтому при вычислении коэффициентов Фурье следует для каждого коэффициента рассматривать два интеграла. В то же время на промежутке 0 < x ≤ 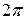 она задана одной функцией. Поэтому для разложения этой функции в ряд Фурье выгоднее поменять пределы интегрирования, приняв
она задана одной функцией. Поэтому для разложения этой функции в ряд Фурье выгоднее поменять пределы интегрирования, приняв 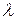 = 0.
= 0.
Найдем коэффициенты Фурье:
а 0 = 
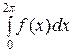 =
= 
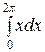 =
= 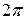 ;
;
ап = 
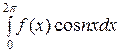 =
= 
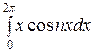 =
= 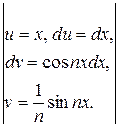 =
=  (
(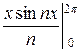 −
−
− 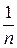
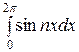 ) =
) = 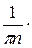
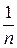
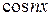
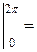
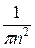 (
(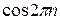 −
− 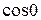 ) = 0;
) = 0;
bп = 
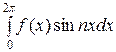 =
= 
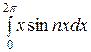 =
= 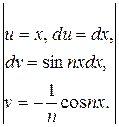 =
=  (
(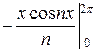 +
+
+ 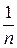
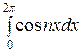 ) =
) =  (
(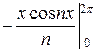 +
+ 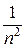
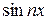
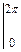 ) =
) = 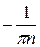 х
х 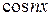
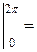
= 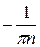 (2 π
(2 π 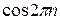 − 0
− 0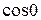 ) =
) = 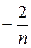 .
.
Тогда разложение будет иметь вид
х = 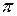 − 2
− 2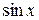 −
− 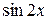 −
− 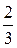
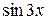 −
− 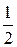
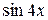 −
− 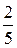
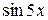 − ….
− ….
Это равенство справедливо во всех точках, кроме точек разрыва, т.е. кроме точек х 0 = 0, ±2 π, ±4 π, ±6 π, … В каждой точке разрыва сумма ряда равна среднему арифметическому ее пределов справа и слева, т.е.
S (x 0)= 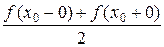 =
= 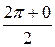 = π.
= π.
■
Ряды Фурье для четных и нечетных функций
Пусть ψ (х) – четная функция. Тогда
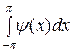 =
= 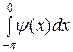 +
+ 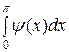 =
= 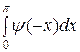 +
+ 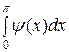 =
= 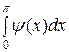 +
+ 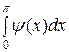 =
=
= 2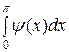 , т.к. ψ (− х) = ψ (х).
, т.к. ψ (− х) = ψ (х).
Аналогично, φ (х) – нечетная функция:
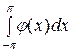 =
= 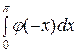 +
+ 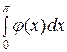 = −
= −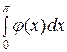 +
+ 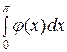 = 0.
= 0.
Если в ряд Фурье разлагается нечетная функция f (х), то произведение f (х)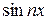 − четная функция, а f (х)
− четная функция, а f (х)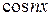 − нечетная функция. Тогда
− нечетная функция. Тогда
а 0 = 
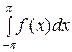 =0,
=0,
ап = 
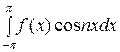 = 0,
= 0,
bп =
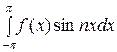 =
=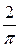
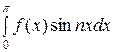 ,
,
т.е. ряд Фурье нечетной функции содержит только “синусы”.
Если в ряд Фурье разлагается четная функция, то произведение f (х)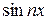 − нечетная функция, а f (х)
− нечетная функция, а f (х)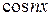 − четная функция. Тогда
− четная функция. Тогда
а 0 = 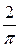
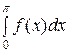 ,
,
ап =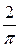
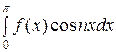 ,
,
bп =
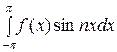 = 0,
= 0,
т.е.ряд Фурье четной функции содержит только “косинусы”.
Представленные формулы позволяют упрощать вычисления при нахождении коэффициентов Фурье.
Так, например, в примере (*) функция f (x) = x, на промежутке − π < x ≤ π является нечетной функцией, поэтому а 0 = 0 и ап = 0.
Ряд Фурье для функции с произвольным периодом 2 L
Пусть f (x) – периодическая функция с периодом 2 L, вообще говоря, отличным от 2 π. Разложим эту функцию в ряд Фурье на отрезке [− L, L ].
Сделаем замену переменных:
х = 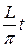 .
.
Тогда функция f (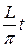 ) будет периодической функцией от t с периодом 2 π. Ее можно разложить в ряд Фурье на отрезке [− π, π ]:
) будет периодической функцией от t с периодом 2 π. Ее можно разложить в ряд Фурье на отрезке [− π, π ]:
f (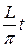 ) =
) =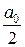 +
+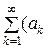
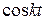 +
+ 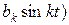 , (1)
, (1)
где
а 0=
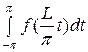 , аk =
, аk =
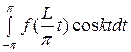 , bk =
, bk = 
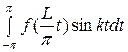 .
.
Возвращаемся к старой переменной х:
х = 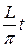 , t =
, t = 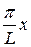 , dt =
, dt = 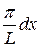 ;
;
пределы интегрирования:
t н = − π, х н = − L, t в = π, х в = L.
Тогда
а 0=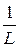
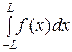 , аk =
, аk =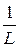
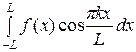 , bk =
, bk = 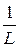
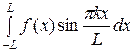 . (2)
. (2)
Ряд (1) примет вид
f ( )=
)=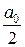 +
+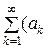
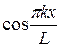 +
+ 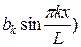 , (3)
, (3)
где коэффициенты а 0, аk, bk вычисляются по формулам (2). Соотношение (3) – ряд Фурье для периодической функции с произвольным периодом 2 L.
Замечание 1. Все сказанное о ряде Фурье для функции с периодом 2 π, справедливо и для рассмотренного ряда.
Замечание 2. Соотношение (3) можно рассматривать как разложение функции в ряд Фурье в общем виде, т.к. при 2 L = 2 π получаем разложение функции с периодом 2 π в ряд Фурье.
Пример. Разложить функцию в ряд Фурье на указанном интервале:
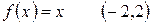 .
.
□
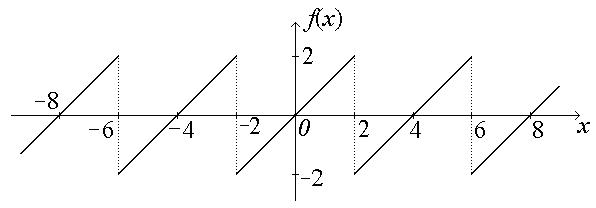
Разложение функции 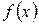 с произвольным периодом 2 L в ряд Фурье имеет вид:
с произвольным периодом 2 L в ряд Фурье имеет вид:
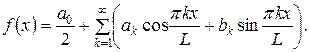
Функция 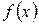 нечетная. Следовательно, коэффициенты
нечетная. Следовательно, коэффициенты 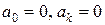 ,и, так как
,и, так как 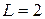 , разложение функции примет вид:
, разложение функции примет вид:
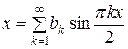 .
.
Найдем коэффициент bk:
bk = 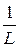
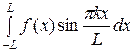 =
= 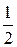
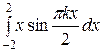 =
= 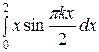 =
= 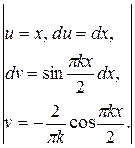 = −
= −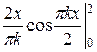 +
+ 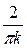
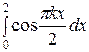 =
= 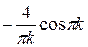 +
+ 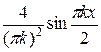
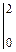 =
= 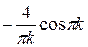 =
=
= 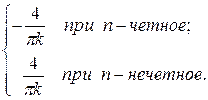 = (−1) k +1
= (−1) k +1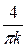 .
.
Тогда разложение будет иметь вид:
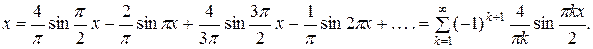
■
Разложение непериодической функции в ряд Фурье
Пусть на отрезке [ a, b ] задана кусочно непрерывная функция f (x). Ее можно разложить в ряд Фурье, если определить любую периодическую кусочно непрерывную функцию f 1(x) с периодом 2 μ ≥ b − a, совпадающую с функцией f (x) на [ a, b ]. Другими словами, функция f (x) доопределяется до функции f 1(x):
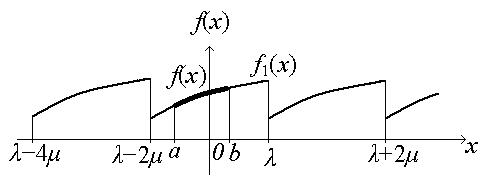
Функцию f 1(x) уже можно разложить в ряд Фурье. Сумма этого ряда во всех точках отрезка [ a, b ] (кроме точек разрыва) совпадает с заданной функцией f (x).
Отметим важный момент. Пусть функция f (x) задана на отрезке [0, L ]. Теперь необходимо ее доопределить на отрезке [− L, 0]. Целесообразно функцию доопределить так, чтобы ее значения в точках отрезка [− L, 0] находились из условия f (x) = f (− x) или f (x) =− f (− x). В первом случае функция f (x) на отрезке [− L, L ] будет четной, а во втором – нечетной. При таком доопределении функции f (x) упрощается нахождение коэффициентов ряда.
Пример. Разложить функцию f (x) = х в ряд Фурье на отрезке [0, π ].
□
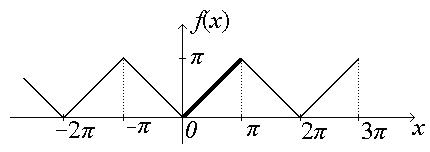
а) Доопределим заданную функцию нечетным образом:
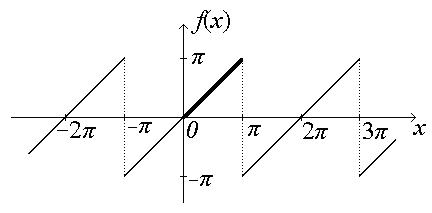
Получили функцию f 1(x) = х с периодом 2 π. Разложение функции  с периодом 2 π в ряд Фурье имеет вид:
с периодом 2 π в ряд Фурье имеет вид:
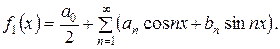
Так как доопределенная функция нечетная, то коэффициенты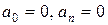 .
.
Тогда разложение функции примет вид:
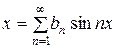 .
.
Согласно примеру (*) bп = (−1) п +1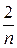 и разложение будет иметь вид
и разложение будет иметь вид
f 1(x) = х = 2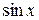 −
− 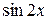 +
+ 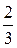
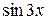 −
−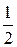
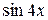 +… =
+… = 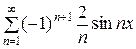 .
.
Функция f 1(x) = х на отрезке [0, π ] совпадает с заданной функцией f (x)= х. Следовательно, заданная функция разложена в ряд Фурье на отрезке [0, π ].
б) Доопределим заданную функцию четным образом:
Получили функцию f 1(x) =| х | с периодом 2 π. Разложение функции 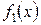 с периодом 2 π в ряд Фурье имеет вид:
с периодом 2 π в ряд Фурье имеет вид:
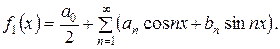
Так как доопределенная функция четная, то коэффициент bn = 0.
Тогда разложение функции примет вид:
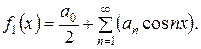
Найдем коэффициенты:
а 0 = 
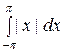 =
= 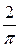
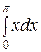 =
= 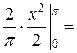 π;
π;
ап = 
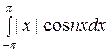 =
= 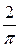
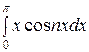 =
= 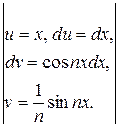 =
= 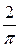 (
(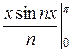 −
− 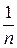
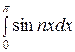 ) =
) =
=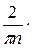
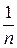
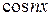
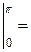
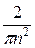 (
(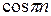 −
− 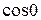 ) =
) = 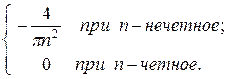
Разложение будет иметь вид
f 1(x) =| х | = 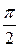 −
− 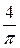
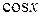 −
− 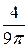
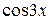 −
− 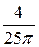
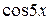 − ….
− ….
Так как доопределенная функция f 1(x) = | х | на отрезке [0, π ] совпадает с заданной функцией f (x) = х, то заданная функция разложена в ряд Фурье на отрезке [0, π ].
■
Интеграл Фурье.
Пусть функция f (x) определена на бесконечном интервале (−∞, +∞) и абсолютно интегрируема на нем, т.е. существует интеграл
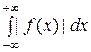 = Q. (1)
= Q. (1)
Пусть f (x) разлагается на любом отрезке [− L, L ] в ряд Фурье:
f ( )=
)=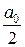 +
+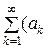
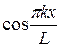 +
+ 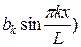 , (2)
, (2)
где
аk = 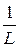
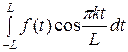 , bk =
, bk = 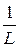
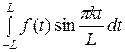 . (3)
. (3)
Подставляя (3) в (2), получим:
f ( ) =
) = 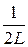
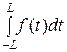 +
+ 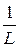
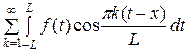 . (4)
. (4)
Пусть
α 1 = 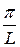 , α 2 =
, α 2 = 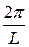 , …, αk =
, …, αk = 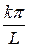 ,…; Δ αk =
,…; Δ αk = 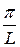 . (5)
. (5)
Подставляя (5) в (4), получим:
f ( ) =
) = 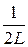
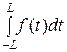 +
+
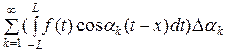 . (6)
. (6)
При L → +∞ первый член в правой части стремится к 0. При любом фиксированном L выражение, стоящее в скобках, есть функция от αk, принимающего значения от 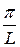 до +∞. Без доказательства: если f (
до +∞. Без доказательства: если f ( ) кусочно непрерывна на каждом конечном интервале, ограничена на бесконечном интервале и удовлетворяет условию (1), то при L → +∞ (6) примет вид:
) кусочно непрерывна на каждом конечном интервале, ограничена на бесконечном интервале и удовлетворяет условию (1), то при L → +∞ (6) примет вид:
f ( )=
)=
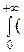
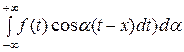 . (7)
. (7)
Стоящее справа выражение называется интегралом Фурье для функции f ( ).
).
Соотношение (7) имеет место для всех точек, где функция непрерывна. В точках разрыва выполняется равенство

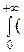
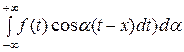 =
= 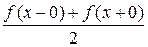 . (
. (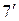 )
)
Вспоминая формулу
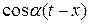 =
= 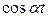
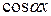 +
+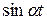
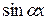 ,
,
запишем (7) в виде
f ( ) =
) = 
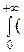
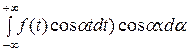 +
+ 
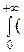
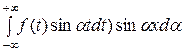 . (8)
. (8)
Каждый из интегралов по t, стоящих в скобках, существует, т.к. функция f ( ) абсолютно интегрируема в интервале (−∞, +∞), а, следовательно, абсолютно интегрируемы и функции f (t)
) абсолютно интегрируема в интервале (−∞, +∞), а, следовательно, абсолютно интегрируемы и функции f (t)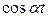 и f (t)
и f (t)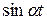 .
.
Рассмотрим частные случаи формулы (8):
1). Пусть f ( ) – четная. Тогда функция f (t)
) – четная. Тогда функция f (t)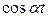 − четная, f (t)
− четная, f (t)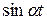 − нечетная и получаем
− нечетная и получаем
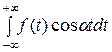 =
= 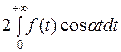 ,
, 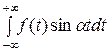 = 0.
= 0.
В этом случае (8) примет вид:
f ( ) =
) = 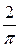
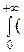
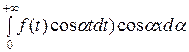 . (9)
. (9)
2). Пусть f ( ) – нечетная. Тогда (8) примет вид:
) – нечетная. Тогда (8) примет вид:
f ( ) =
) = 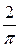
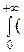
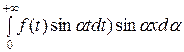 . (10)
. (10)
Если функция f ( ) определена только на интервале (0, +∞), то ее можно представить при х > 0 как формулой (9), так и (10). В первом случае мы ее доопределяем на интервале (−∞, 0) четным образом, а во втором − нечетным.
) определена только на интервале (0, +∞), то ее можно представить при х > 0 как формулой (9), так и (10). В первом случае мы ее доопределяем на интервале (−∞, 0) четным образом, а во втором − нечетным.
Отметим, что в точках разрыва вместо выражения f ( ) в левых частях (9) и (10) следует писать выражение
) в левых частях (9) и (10) следует писать выражение
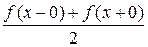 .
.
Рассмотрим формулу (8). Интегралы, стоящие в скобках являются функциями от α.
Пусть А (α) = 
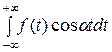 , В (α) =
, В (α) = 
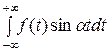 .
.
Тогда (8) примет вид:
f ( )=
)=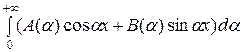 (11)
(11)
Говорят, что формула (11) дает разложение f ( ) на гармоники с непрерывно меняющейся от 0 до +∞ частотой α. Закон распределения амплитуд и начальных фаз в зависимости от частоты α выражается через функции А (α) и В (α).
) на гармоники с непрерывно меняющейся от 0 до +∞ частотой α. Закон распределения амплитуд и начальных фаз в зависимости от частоты α выражается через функции А (α) и В (α).
Рассмотрим формулу (9):
Пусть
F (α) = 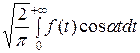 . (12)
. (12)
Тогда (9) запишется в виде:
f ( ) =
) = 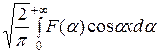 . (13)
. (13)
Функция F (α) называется косинус-преобразованием Фурье для функции f ( ) (прямое преобразование).
) (прямое преобразование).
Если в (12) считать F (α) заданной, а f (t) искомой функцией, то оно является интегральным уравнением для функции f (t). Формула (13) дает решение этого уравнения (обратное преобразование).
Аналогично, на основании (10) можно записать:
Φ (α) = 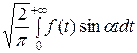 , (14)
, (14)
f ( ) =
) = 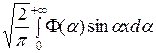 . (15)
. (15)
Функция Φ (α) называется синус-преобразованием Фурье для функции f ( ) (прямое преобразование). Формула (15) – обратное преобразование.
) (прямое преобразование). Формула (15) – обратное преобразование.
Пример. Найти косинус- и синус-преобразования функции f ( ) =
) = 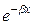 , (β > 0, x ≥ 0).
, (β > 0, x ≥ 0).
□
Определим косинус-преобразование Фурье:
F (α) = 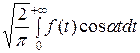 =
=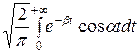 =!
=!
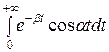 =
=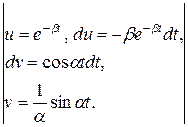 =
= 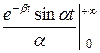 +
+ 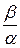
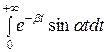 =
=
=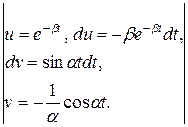 =
=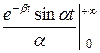 +
+ 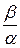 (−
(−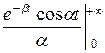 −
− 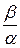
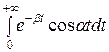 ) =
) =
= 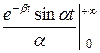 −
− 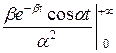 −
− 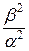
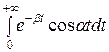 ;
;
(1+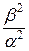 )
)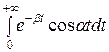 = (
= (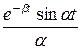 −
− 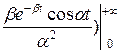 ;
;
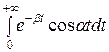 =
=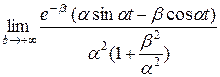
 =
= 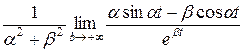
 =
=
= 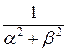 (0 − (0 − β)) =
(0 − (0 − β)) = 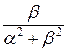 .
.
! = 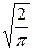
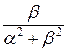 .
.
Аналогично найдем синус-преобразование Фурье:
Φ (α) = 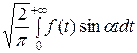 =
= 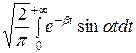 =
= 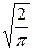
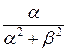 .
.
По формулам (13) и (15) запишем взаимные соотношения:
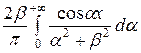 =
= 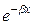 ,
, 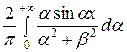 =
= 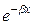 .
.
■
 2014-02-09
2014-02-09 5257
5257
