Задания для самостоятельной работы. Составить программы для решения следующих задач

«ВЕКТОРЫ»

Составить программы для решения следующих задач:

Варианты заданий:

Вариант 1.

1. Среди N треугольников с заданными сторонами подсчитать количество прямоугольных, среди которых определить треугольник с наибольшей площадью.

2. Даны целые числа 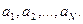Удалить из последовательности все члены со значением max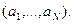

3. Дана действительная матрица размера NxM. Определить, имеются ли в ней столбцы со знакочередующимися элементами.

4. Отсортировать целочисленную квадратную матрицу порядка 5 в порядке убывания сумм положительных элементов столбцов.

Вариант 2.

1. Среди N четырехугольников с заданными сторонами и одной диагональю определить ромбы, среди которых выбрать ромб с наибольшей площадью.

2. Даны натуральные числа 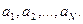Отсортировать последовательность в порядке возрастания количеств цифр “1”, встречающихся в записи чисел.

3. Дана действительная матрица размера NxM. Получить последовательность 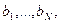где b_k – это сумма наибольшего и наименьшего из значений элементов k -й строки.

4. Проверить, имеются ли в целочисленной матрице размера 5х4 строки, целиком состоящие из четных элементов.

Вариант 3.

1. Среди N треугольников, у которых известна одна сторона и прилежащие к ней углы, определить равнобедренные, и среди них найти треугольник с самой большой стороной.

2. Определить, имеется ли в массиве целых чисел 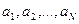хотя бы одно число, в записи которого встречается цифра “0”.

3. Дана целочисленная квадратная матрица порядка N. Найти номера столбцов, элементы в каждой из которых одинаковы.

4. Строки действительной матрицы размера 6х4, отсортированные по возрастанию, расположить в начале матрицы, сохраняя исходный взаимный порядок как среди упорядоченных, так и среди остальных строк.

Вариант 4.

1. Среди N квадратных уравнений с заданными коэффициентами определить уравнение с наибольшим корнем.

2. Из массивов целых чисел 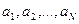и 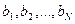убрать элементы, удовлетворяющие условию 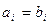, где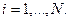

3. Определить минимальный элемент среди максимальных элементов столбцов целочисленной матрицы размера 4х5.

4. Дана действительная квадратная матрица порядка N. Получить последовательность 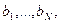где b_k – это значение первого по порядку положительного элемента k -ой строки (если таких элементов нет, то принять b_k =-1).

Вариант 5.

1. Среди N четырехугольников с заданными сторонами подсчитать количество параллелограммов, из которых найти один с наибольшим периметром.

2. Дан массив целых положительных чисел 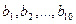. Отсортировать массив по возрастанию количеств цифр, встречающихся в записи чисел.

3. Дана целочисленная квадратная матрица порядка N. Найти номера строк, элементы каждой из которых образуют убывающую или возрастающую последовательность.

4. В данной действительной матрице размера 5х4 поменять местами строку, содержащую элемент с наибольшим значением, со строкой, содержащей элемент с наименьшим значением. Предполагается, что эти элементы единственны.

Вариант 6.

1. Среди N треугольников, заданных двумя сторонами и углом между ними, определить количество равносторонних, из которых найти наименьший.

2. Дан массив целых чисел 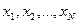. Преобразовать массив по следующему правилу: все отрицательные элементы перенести в его начало, а все остальные – в конец, сохраняя исходное расположение как среди отрицательных, так и среди остальных элементов.

3. Определить, в какой строке (строках) действительной матрицы размера 6х5 имеется наибольшее количество отрицательных элементов.

4. Дана действительная квадратная матрица В порядка N. Получить для нее транспонированную матрицу В^Т.

Вариант 7.

1. Среди N квадратных уравнений с заданными коэффициентами подсчитать количество уравнений, имеющих различные действительные корни, определить среди них уравнение с наименьшим корнем.

2. Определить, имеется ли в массиве целых положительных чисел 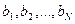число, в котором первая и последняя цифры совпадают. Выдать на экран само число и его номер.

3. Дана действительная матрица размера MxN. Определить числа 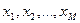, равные соответственно суммам наибольших и наименьших значений элементов строк.

4. В целочисленной квадратной матрице порядка 5 все строки, состоящие только из положительных элементов расположить в конце, сохраняя исходное расположение как среди положительных, так и среди остальных строк.

Вариант 8.

1. Среди N треугольников с заданными сторонами определить разносторонние, из которых найти треугольник с наибольшей стороной.

2. Дан массив целых положительных чисел 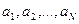. Вставить в него после каждого числа, состоящего из одинаковых цифр, такое же число.

3. Дана квадратная вещественная матрица А порядка N. Получить матрицу А².

4. Расположить строки целочисленной матрицы размера 4х5 в порядке убывания количеств положительных элементов в строках.

Вариант 9.

1. Среди N треугольников с известными сторонами выделить прямоугольные, среди них определить треугольник с наибольшей высотой, опущенной на гипотенузу.

2. Даны два целочисленных массива 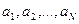и 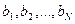. Отсортировать эти массивы по убыванию разностей 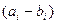, где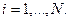

3. Дана целочисленная матрица размера 4х6. Определить количество “особых” элементов матрицы, считая элемент “особым”, если он больше суммы остальных элементов своего столбца.

4. Найти минимальное из произведений элементов строк действительной квадратной матрицы порядка N.

Вариант 10.

1. Среди N параллелограммов с известными сторонами и одной диагональю выделить ромбы, среди них определить ромб с наибольшей диагональю.

2. Дан массив целых положительных чисел. Разместить в начале массива числа, содержащие цифру “0”, сохраняя исходное расположение как среди чисел с “0”, так и среди остальных чисел.

3. Определить, является ли целая квадратная матрица 5-го порядка симметричной (относительно главной диагонали).

4. Дана действительная матрица размера NxM. Упорядочить ее строки по убыванию абсолютных величин ее элементов.

Вариант 11.

1. Даны координаты N точек – вершин ломаной линии на плоскости. Найти длину ломаной и определить ее самое длинное звено.

2. Дан массив целых положительных чисел 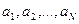. Удалить из него все числа, у которых все цифры, встречающиеся в их записи, одинаковы.

3. Подсчитать количество строк целой матрицы размера 4х6, в которых все элементы, находящиеся в столбцах с четными номерами, нечетны.

4. Дана целая квадратная матрица порядка N. Определить, является ли она “магическим квадратом”, т.е. такой, в которой суммы элементов во всех строках и столбцах одинаковы.

Вариант 12.

1. Даны координаты N точек в трехмерном пространстве. Определить точку, наиболее удаленную от точки с заданными координатами.

2. В массиве целых положительных чисел 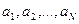разместить в начале массива числа, в записи которых первая цифра “1”, сохраняя исходное расположение как среди чисел с “1”, так и среди остальных чисел.

3. Выделить в действительной матрице размера 4х5 столбцы, полностью состоящие из знакочередующихся элементов, среди них найти столбец с наибольшей суммой.

4. Дана действительная квадратная матрица порядка N. Подсчитать количество “особых” элементов матрицы, считая элемент ”особым”, если в его строке слева от него находятся элементы, меньшие его, а справа – большие.

Вариант 13.

1. Даны N прямоугольных треугольных призм. Определить призму с наибольшей поверхностью.

2. Упорядочить массив целых положительных чисел 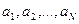в порядке убывания сумм цифр, встречающихся в их записи.

3. Получить произведение минимальных элементов столбцов действительной матрицы размера 4х5.

4. Дана целочисленная квадратная матрица порядка N. Найти номера строк, элементы которых образуют симметричные последовательности (палиндромы).

Вариант 14.

1. Среди четырехугольников с известными сторонами подсчитать количество прямоугольников, среди которых определить прямоугольник с наибольшим периметром.

2. Дан массив целых положительных чисел 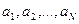. Числа, у которых все цифры, встречающиеся в их записи, находятся в порядке возрастания, перенести в конец массива, сохраняя исходное расположение как среди этих, так и среди остальных чисел.

3. Дана целочисленная квадратная матрица порядка N. Получить последовательность 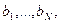где b_k – это наименьшее из значений элементов, находящихся в начале k -

ой строки матрицы до элемента, принадлежащего главной диагонали, включительно.

4. Дана действительная квадратная матрица порядка N. Отсортировать элементы каждого столбца в порядке убывания значений его элементов.

Вариант 15.

1. Даны координаты N точек на плоскости. Найти номера всех пар точек, расстояние между которыми наибольшее.

2. Дан массив целых положительных чисел 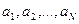. Преобразовать массив путем сдвига его элементов на k позиций влево (k >0).

3. Определить все седловые точки (если таковые вообще имеются) в действительной матрице размера 5х6. Элемент матрицы называется седловой точкой, если он является одновременно наименьшим в своей строке и наибольшим в своем столбце.

4. Дана целая квадратная матрица порядка N. Определить количество различных элементов матрицы (т.е. повторяющиеся элементы считать один раз).