2015-03-27
702
Теория теплоемкости кристаллических тел была разработана А. Эйнштейном в 1907г. Согласно этой модели атомы совершают гармонические колебания независимо друг от друга. Колебания атомов не связаны между собой.
Колебания атомов описывают уравнения Шредингера.
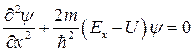- уравнение Шредингера.
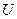- потенциальная энергия, 
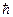- постоянная Планка.
, 
.
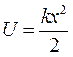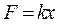Частота колебаний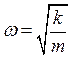 
, 
.
.
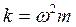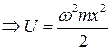В разделе квантовая механика рассматривается решение такого уравнения. Одним из выводов является выражение для энергии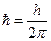 
.
, 
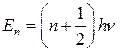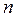- это величина, принимающая набор целых значений.
Запишем выражение для статистической суммы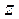 
:
.
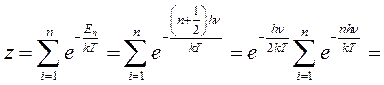
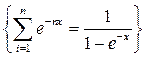
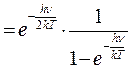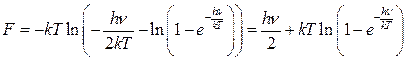
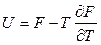(из формулы Гиббса – Геймгольца)
.
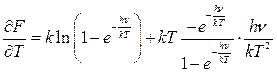
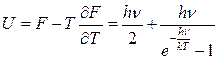с учетом колебания вдоль только оси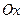 
для одного атома.
Если учесть, что всего атомов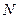 
, а число степеней свободы равно трем, то внутреннюю энергию кристалла запишем в виде:
.
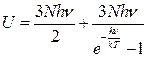Выражение для 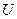позволяет найти выражение для 
.
, 
.
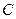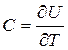
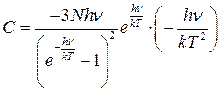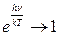Выделим два случая:
1) 
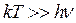
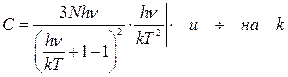
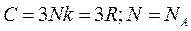
Рассмотрим случай, когда температуры низкие. Если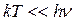 
, то величина экспоненты значительно больше.
2) .
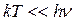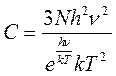, при температурах, близких к 0.
Но значительно быстрее изменяется функция экспоненты. Следовательно, экспонента задает характер изменения температуры, что противоречит экспоненте.
В 1912г Дебай усовершенствовал модель Эйнштейна. Суть поправки Дебая: атомы кристаллической решетки совершают не независимые, а зависимые колебания. Тогда энергия кристалла можно рассматривать как сумму.
.
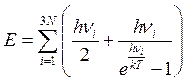Анализ этой формулы позволяет провести аналогию с формулой Планка для излучения абсолютно черного тела. И в формуле Планка и в формуле Дебая сумма порций энергии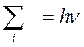 
.
В случае твердых тел порции энергии называются фонон.
Принципиальная разни ца между фотонами и фононами: для распространения фотонов среда не нужна, а для распространения фононов наличие среды обязательно.
Дебай представляет следующую формулу для внутренней энергии:
, 
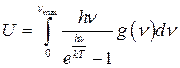
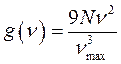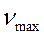- это максимальная частота колебаний, при которой тело еще сохраняет твердую форму.
,
.
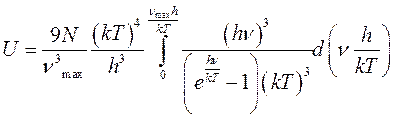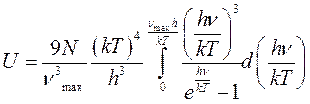а)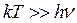 
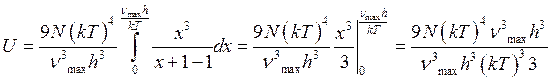
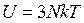
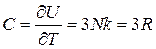
б)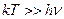 
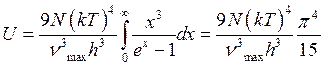
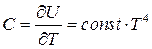этот результат дает экспериме
