Задача 20. Найти общее решение дифференциального уравнения 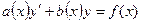 и частное решение, удовлетворяющее начальному условию
и частное решение, удовлетворяющее начальному условию 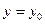 при
при 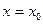 .
.
20.1. 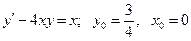 .
.
20.2. 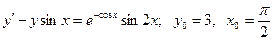 .
.
20.3. 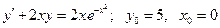 .
.
20.4. 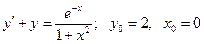 .
.
20.5. 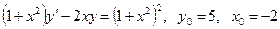 .
.
20.6. 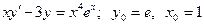 .
.
20.7. 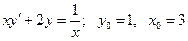 .
.
20.8. 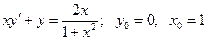 .
.
20.9. 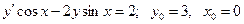 .
.
20.10. 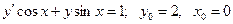 .
.
Задача 21. Найти общее решение дифференциального уравнения
21.1. 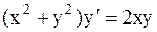 . 21.2.
. 21.2. 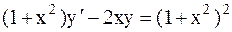 .
.
21.3. 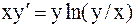 . 21.4.
. 21.4. 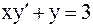 .
.
21.5. 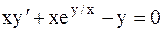 . 21.6.
. 21.6. 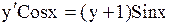 .
.
21.7. 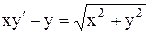 . 21.8.
. 21.8. 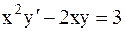 .
.
21.9. 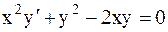 . 21.10.
. 21.10. 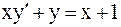 .
.
Задача 22. Найти общее решение дифференциального уравнения 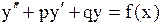 и частное решение, удовлетворяющее начальным условиям
и частное решение, удовлетворяющее начальным условиям 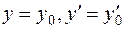 при
при 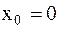 .
.
22.1. 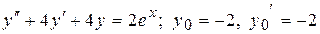 .
.
22.2. 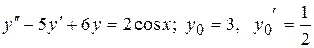 .
.
22.3. 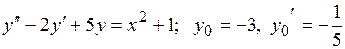 .
.
22.4. 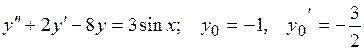 .
.
22.5. 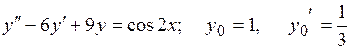 .
.
22.6. 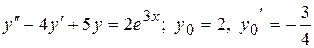 .
.
22.7. 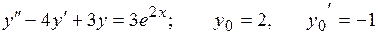 .
.
22.8. 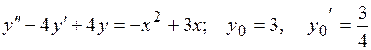 .
.
22.9. 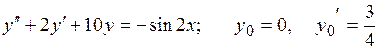 .
.
22.10. 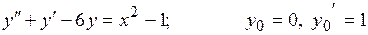 .
.
Задача 23. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям 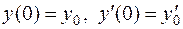 .
.
23.1. 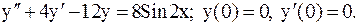
23.2. 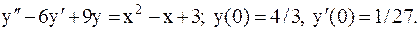
23.3. 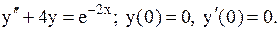
23.4. 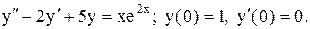
23.5. 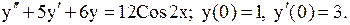
23.6. 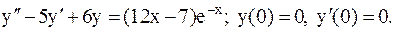
23.7. 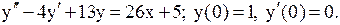
23.8. 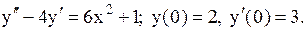
23.9. 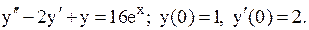
23.10. 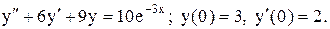
Ряды
Задача 24. Исследовать сходимость числового ряда 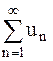 .
.
24.1. 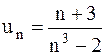 . 24.2.
. 24.2. 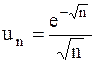 .
.
24.3. 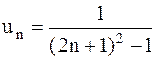 . 24.4.
. 24.4. 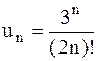 .
.
24.5. 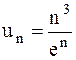 . 24.6.
. 24.6. 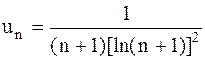 .
.
24.7. 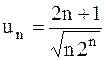 . 24.8.
. 24.8. 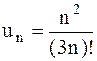 .
.
24.9. 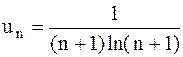 . 24.10.
. 24.10. 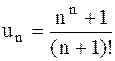 .
.
Задача 25. Найти интервал сходимости степенного ряда 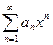 .
.
25.1. 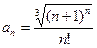 . 25.2.
. 25.2. 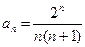 .
.
25.3. 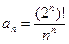 . 25.4.
. 25.4. 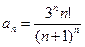 .
.
25.5. 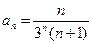 . 25.6.
. 25.6. 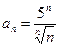 .
.
25.7. 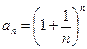 . 25.8.
. 25.8. 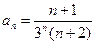 .
.
25.9. 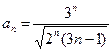 . 25.10.
. 25.10. 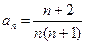 .
.
Задача 26. Написать три первых члена степенного ряда по заданному общему члену 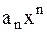 , где
, где 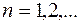 ; найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала.
; найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала.
26.1. 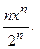 26.2.
26.2. 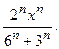 26.3.
26.3. 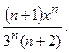 26.4.
26.4. 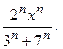 26.5.
26.5. 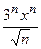
26.6. 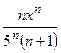 26.7.
26.7. 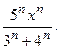 26.8.
26.8. 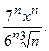 26.9.
26.9. 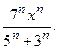 26.10.
26.10. 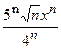
Задача 27. Вычислить определенный интеграл 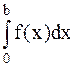 с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.
с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.
27.1. 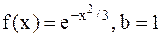 . 27.2.
. 27.2. 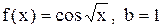 .
.
27.3. 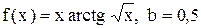 . 27.4.
. 27.4. 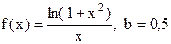 .
.
27.5. 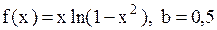 . 27.6.
. 27.6. 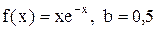 .
.
27.7. 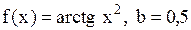 . 27.8.
. 27.8. 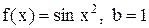 .
.
27.9. 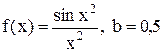 . 27.10.
. 27.10. 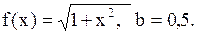
Задача 28. Выразить определенный интеграл 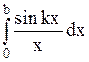 в виде сходящего ряда, используя ряд Маклорена для подынтегральной функции. Найти приближенное значение этого интеграла с точностью до
в виде сходящего ряда, используя ряд Маклорена для подынтегральной функции. Найти приближенное значение этого интеграла с точностью до 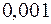 .
.
28.1. 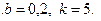 28.2.
28.2. 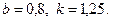 28.3.
28.3. 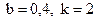
28.4. 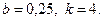 28.5.
28.5. 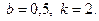
Выразить определенный интеграл 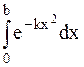 в виде сходящегося ряда, используя ряд Маклорена для подынтегральной функции. Найти приближенное значение этого интеграла с точностью до 0,001.
в виде сходящегося ряда, используя ряд Маклорена для подынтегральной функции. Найти приближенное значение этого интеграла с точностью до 0,001.
28.6. 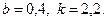 28.7.
28.7. 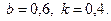 28.8.
28.8. 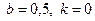
28.9. 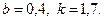 28.10.
28.10. 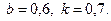
 2015-03-07
2015-03-07 821
821








