Непрерывность функции

Пусть функция 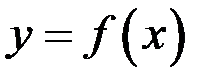определена в некоторой окрестности точки .

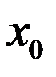Определение. Функция 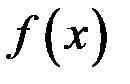называется непрерывной в точке 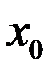, если она имеет предел в точке 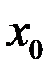и этот предел равен 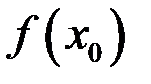– значению функции 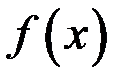в точке :

.

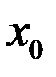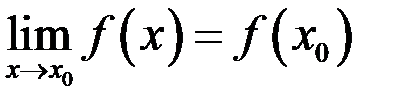Таким образом, для того чтобы функция 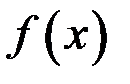была непрерывна в точке 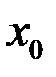, необходимо и достаточно выполнение трех условий:

1) функция 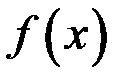должна быть определена в точке ;

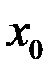2) должны существовать пределы функци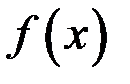и при 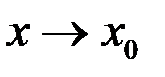как слева, так и справа, т.е. 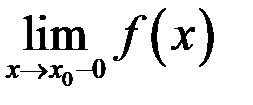и ;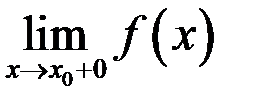

3) эти пределы должны быть равны между собой и равны значению функции 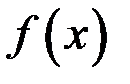в точке 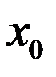, т.е. .

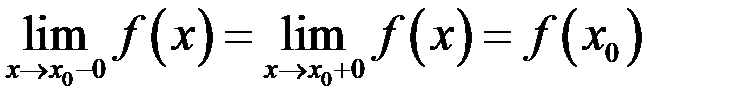Если хотя бы одно из этих условий не выполнено, то говорят, что функция имеет разрыв в точке 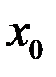и точку 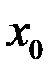называют точкой разрыва функции .

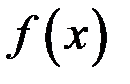Точки разрыва следует искать среди точек, не входящих в область определения функции.