Если 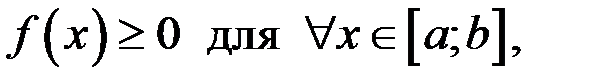 то
то 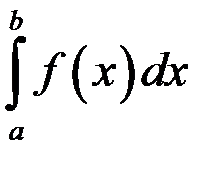 численно равен площади криволинейной трапеции, ограниченной кривой
численно равен площади криволинейной трапеции, ограниченной кривой 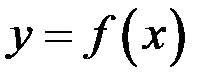 ,
,
прямыми 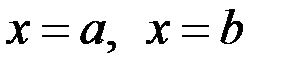 и осью ох:
и осью ох:
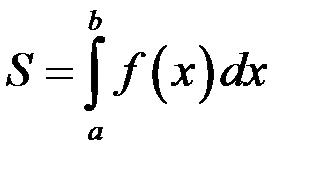
Если 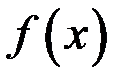 меняет знак конечное число раз на отрезке
меняет знак конечное число раз на отрезке 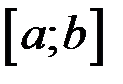 , то интеграл по всему отрезку разбивается на сумму интегралов по частичным отрезкам, интеграл будет положителен там, где
, то интеграл по всему отрезку разбивается на сумму интегралов по частичным отрезкам, интеграл будет положителен там, где 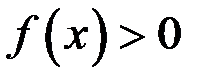 и отрицателен, где
и отрицателен, где 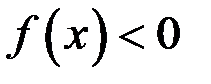 :
:
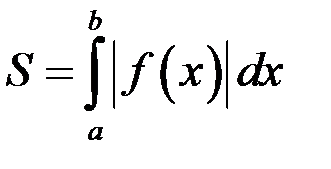 .
.
Пусть нужно вычислить площадь фигуры, ограниченной кривыми 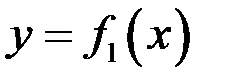 и
и 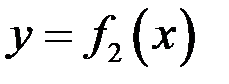 и прямыми
и прямыми 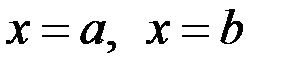 , тогда при условии
, тогда при условии 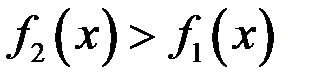 имеем
имеем
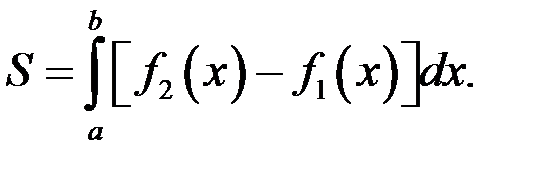
 2015-03-07
2015-03-07 409
409








