Пусть функция 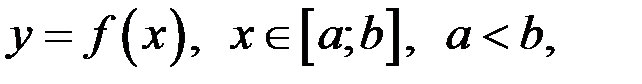 определена и непрерывная на отрезке
определена и непрерывная на отрезке 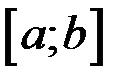 и пусть, для определенности,
и пусть, для определенности, 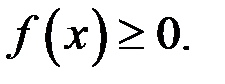
Разобьем отрезок 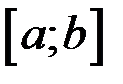 на n частей произвольным образом точками деления:
на n частей произвольным образом точками деления: 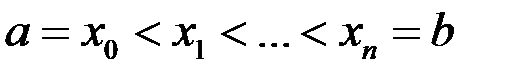 . Выберем на каждом частичном промежутке
. Выберем на каждом частичном промежутке 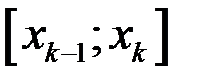 произвольным образом точки
произвольным образом точки 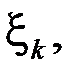
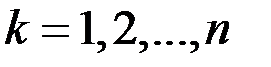 .
.
Обозначим 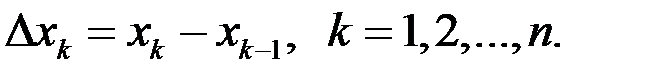 Составим сумму
Составим сумму 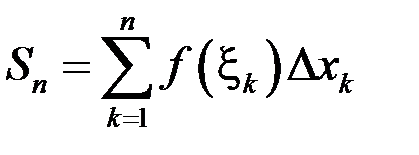 , которая называется интегральной суммой для функции
, которая называется интегральной суммой для функции 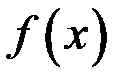 на отрезке
на отрезке 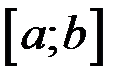 .
.
Обозначим длину наибольшего частичного промежутка через 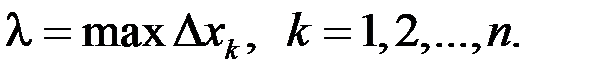 Перейдем к пределу при
Перейдем к пределу при 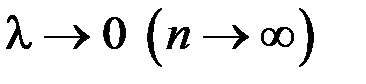 .
.
Если существует конечный предел 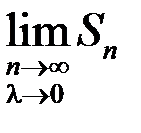 , не зависящий от способа разбиения отрезка
, не зависящий от способа разбиения отрезка 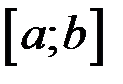 на частичные и выбора на них точек
на частичные и выбора на них точек 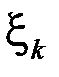 , то он и называется определенным интегралом от функции
, то он и называется определенным интегралом от функции 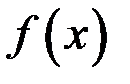 на отрезке
на отрезке 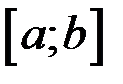 и обозначается
и обозначается
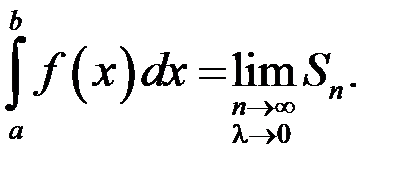
Если 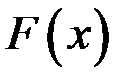 – любая первообразная для функции
– любая первообразная для функции 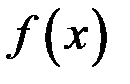 , то справедлива формула Ньютона – Лейбница:
, то справедлива формула Ньютона – Лейбница:
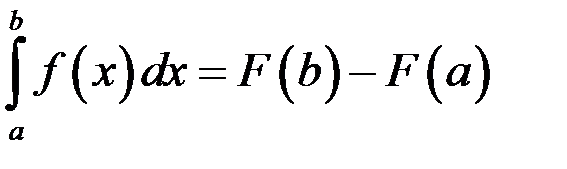 ,
,
т.е. для вычисления определенного интеграла от непрерывной функции 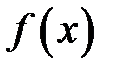 нужно составить разность значений произвольной ее первообразной для верхнего и нижнего пределов интегрирования.
нужно составить разность значений произвольной ее первообразной для верхнего и нижнего пределов интегрирования.
 2015-03-07
2015-03-07 397
397








