Задача 14. Результаты обследования семей по числу членов оказались таким 2; 5; 3; 4; 1; 3; 6; 2; 4; 3; 4; 1; 3; 5; 2; 3; 4; 4; 3. Получить по этим данным вариационный ряд и построить полигон распределения относительных частот.
Решение. Проведем ранжирование ряда. Для этого перепишем результаты наблюдений в порядке возрастания вариант:
1; 1; 2; 2; 2; 3; 3: 3; 3; 3; 3; 3; 4; 4; 4; 4; 4; 5; 5; 6.
Определяем частоты различных вариант. Варианта 1 встречается два раза. Следовательно, ее частота равна m 1 = 2. Варианта 2 встречается три раза. Следовательно, ее частота равна m 2 = 3. Аналогично получаем m 3 = 7, m 4 = 5, m 5 = 2, m 6 = 1.
Определяем относительные частоты наблюдавшихся в выборке вариант. Они равны отношению соответствующей частоты варианты к общему числу наблюдений. Имея в виду, что общее число наблюдений (объем выборки) равно n = 20, относительная частота варианты 1 будет равна 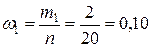 . Аналогично
. Аналогично
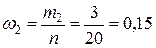 ,
, 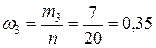 ,
, 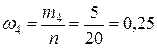 ,
,
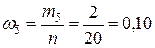 ,
, 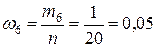 .
.
Проверяем правильность расчетов. Для этого суммируем относительные частоты
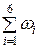 = 0,10 + 0,15 + 0,35 + 0,25 + 0,10 + 0,05 = 1,00.
= 0,10 + 0,15 + 0,35 + 0,25 + 0,10 + 0,05 = 1,00.
Сумма всех относительных частот равна единице, следовательно, вычисления произведены верно. Результаты вычислений сводим в таблицу 2, которая называется вариационным рядом или рядом распределения.
Таблица 2 –Распределение числа членов семьи
| Значения варианты хi | ||||||
| Частота варианты mi | ||||||
| Относительная частота варианты ωi | 0,10 | 0,15 | 0,35 | 0,25 | 0,10 | 0,05 |
Зависимость относительных частот варианты от ее значения изобразим на графике (рис. 4). Концы ординат относительных частот соединяем прямыми линиями. Полученный график называется полигоном распределения относительных частот.
 |
ωi



 0,3
0,3
 |
 0,2
0,2
 |




 0,1
0,1
 |
0 1 2 3 4 5 6 x
Рисунок 4 – Полигон распределения относительных частот
Задача 15. Известны урожайности в центнерах на один гектар яровой пшеницы в 20 хозяйствах: 13,9; 12,4; 13,1; 6,3; 11,8; 11,6; 10,5; 10,4; 10,6; 11,3; 15,1; 11,7; 11,3; 10,2; 11,0; 10,7; 8,2; 9,6; 10,2; 15,1. Получить интервальный ряд распределения и начертить гистограмму.
Решение. Записываем исходные данные в виде ранжированного ряда: 6,3; 8,2; 9,6; 10,2; 10,2; 10,4; 10,5; 10,6; 10,7; 11,0; 11,3; 11,3; 11,6; 11,7; 11,8; 12,4; 13,1; 13,9; 15,1; 15,1.
Рассматривая этот ряд, видим, что диапазон изменения вариант в выборке составляет 6 – 16.
Весь диапазон изменения вариант в выборке разбиваем на несколько интервалов. Размер интервала выбирается произвольно, но следует иметь в виду, что чем меньше интервал, тем точнее результаты. Принимаем размер интервала равным 2 единицам (∆ xi = 2). Получаем пять интервалов: 6 – 8, 8 – 10, 10 – 12, 12- 14, 14 – 16.
Определяем частоту попадания вариант выборки в каждый интервал. В первый интервал попадает одно значение (6,3) из ряда, поэтому m 1 = 1. Во второй попадает два значения (8,2 и 9,6), поэтому m 2 = 2. Аналогично получаем m 3 = 12, m 4 = 3, m 5 = 2.
Определяем относительные частоты попадания вариант выборки в каждый интервал:
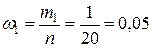 ,
, 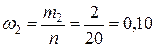 ,
, 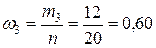 ,
,
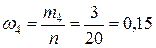 ,
, 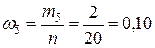 .
.
Проверяем правильность расчетов. Для этого суммируем относительные частоты: 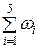 = 0,05 + 0,10 + 0,60 + 0,15 + 0,10 = 1,00.
= 0,05 + 0,10 + 0,60 + 0,15 + 0,10 = 1,00.
Сумма всех относительных частот равна единице, следовательно, вычисления произведены правильно.
Определяем плотность относительных частот вариант как отношение относительной частоты ωi к размеру интервала ∆ xi:
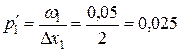 ,
, 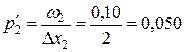 ,
, 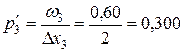 ,
,
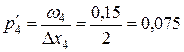 ,
, 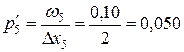 .
.
Результаты вычислений поместим в таблицу 3.
Таблица 3 – Интервальный ряд распределения урожайности яровой пшеницы
| Интервал значений урожайности ∆ хi | 6 - 8 | 8 - 10 | 10 - 12 | 12 - 14 | 14 - 16 |
| Частота варианты mi | |||||
| Относительная частота варианты ωi | 0,05 | 0,10 | 0,60 | 0,15 | 0,10 |
Плотность относительных частот 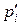 | 0,025 | 0,050 | 0,300 | 0,075 | 0,050 |
Выполняем построение графика показывающего зависимость плотности относительных частот от значений вариант.
 |
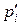



 0,3
0,3
 0,2
0,2



 0,1
0,1
 |
0 6 8 10 12 14 16 x
Рисунок 5 – Гистограмма распределения плотности относительных частот
По горизонтальной оси наносим шкалу возможных значений вариант, по оси ординат – плотность относительных частот. Получаем столбчатую диаграмму, которая называется гистограммой распределения плотности относительных частот.
Задача 16. Даны величины 25 единиц выборки: 9; 11; 9; 6; 6; 7; 6; 8; 9; 9; 11; 10; 6; 7; 6; 8; 9; 10; 4; 9; 10; 7; 8; 9; 6. Определить: 1) величину, которую следует принять за среднюю генеральной совокупности; 2) величину, которую следует принять за дисперсию генеральной совокупности; 3) доверительный интервал с границами 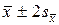 .
.
Решение. Приближенное значение средней генеральной совокупности равно среднему арифметическому значению выборки
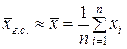 .
.
Для оценки дисперсии генеральной совокупности используем формулу
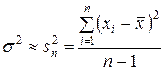 .
.
Расчеты по приведенным формулам сведем в таблицу 4.
Таблица 4 – Результаты расчетов отклонений
.
| № п/п | Результат наблюде- ния x i | 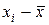 | 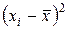 | № п/п | Результат наблюде- ния xi | 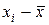 | 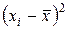 |
| -1 | |||||||
| -2 | |||||||
| -2 | |||||||
| -2 | |||||||
| -1 | -4 | ||||||
| -2 | |||||||
| -1 | |||||||
| -2 | |||||||
| -2 | 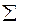 |
Среднее квадратическое отклонение выборочной средней найдем по формуле
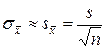 .
.
1) В качестве средней генеральной совокупности принимаем величину
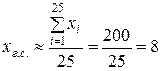 ;
;
2) в качестве дисперсии генеральной совокупности имеем величину
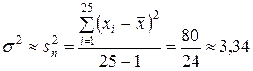 ;
;
3) доверительный интервал размером ±2 средних квадратических отклонений:
среднее квадратическое отклонение средней выборки
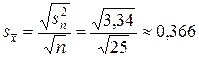 ,
,
Отсюда, доверительный интервал
8 ± 2∙0,366, или 8 ± 0,732.
1. Что такое выборка? Как обеспечивается представительность ее?
2. Объясните, как получается вариационный ряд распределения.
3. Как составляется интервальный ряд и строится гистограмма?
4. Что называется дисперсией генеральной совокупности?
Рекомендуемая литература и интернет-ресурс
1. Зайцев И.А. Высшая математика: Учеб. для вузов. М. Дрофа. 2005. – 398 с.
2. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. М. «Издательство АСТ». 2001. 656 с.
3. Письменный Д.Т. Конспект лекций по высшей математике М., Айрис пресс. 2011. 608 с.
4. Гмурман В.Е. Теория вероятностей и математическая статистика: Учебное пособие для вузов. М. Высшая школа. 2003. – 479 с.
5. www.exponenta.ru – образовательный математический сайт.
6. www.mathserfer.com – помощь в решении заданий.
7. www.allmatematika.ru – консультации по математике.
 2015-03-07
2015-03-07 18498
18498
