Энергия магнитного поля

Проводник, по которому протекает электрический ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезновением тока. Магнитное поле, подобно электрическому полю, является носителем энер­гии. Естественно предположить, что энер­гия магнитного поля равна работе, которая затрачивается током на создание этого поля.

Рассмотрим контур с индуктивностью 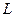, по которому течет ток 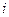. С контуром сцеплено магнитное потокосцепление (15.6) 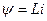, причем при изменении тока на 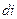потокосцепление изменяется на 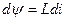. Для изменения магнитного потокосцепления на 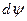необходимо совершить работу 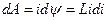. Тогда работа, равная энергии магнитного поля

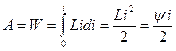. (15.26)

Рассмотрим магнитное поле внутри длинного соленоида сечением 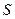с числом витков 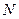и длиной 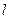. Подставив в (15.26) формулу (15.7), найдем

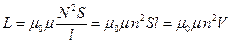, (15.7)

где 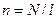- число витков на единицу длины, 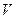- объем соленоида, получим:

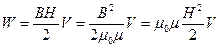. (15.27)

Здесь учтено, что магнитная индукция соленоида 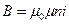, а напряженность его магнитного поля .

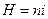Магнитное поле длинного соленоида однородно и сосредоточено внутри него, поэтому энергия (15.27) распределена в соленоиде с постоянной объемной плотностью

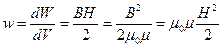. (15.28)

Напомним, что объемная плотность энергии электростатического поля равна

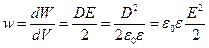. (11.31)

Сравнивая (15.28) c (11.31) видно, что эти формулы дуальны (подобны) друг другу. Формула (15.28) выведена для однородного поля соленоида, но она справедлива и для любых неоднородных магнитных линейных полей.