Если по замкнутому контуру протекает переменный ток 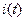 , то магнитное поле с изменяющимся потоком создается собственным током в этом контуре, и в соответствии с законом электромагнитной индукции, в контуре возникает дополнительная ЭДС, называемая ЭДС самоиндукции.
, то магнитное поле с изменяющимся потоком создается собственным током в этом контуре, и в соответствии с законом электромагнитной индукции, в контуре возникает дополнительная ЭДС, называемая ЭДС самоиндукции.
ЭДС самоиндукции равна взятой с обратным знаком скорости изменения потокосцепления 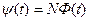 :
:
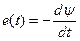 , (15.5)
, (15.5)
где 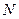 - число витков контура,
- число витков контура, 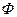 - поток, пронизывающий один виток.
- поток, пронизывающий один виток.
Потокосцепление 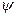 пропорционально току
пропорционально току 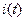 :
:
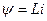 ,
, 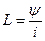 , (15.6)
, (15.6)
где 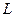 - индуктивность контура, зависящая от геометрии контура и числа витков
- индуктивность контура, зависящая от геометрии контура и числа витков 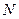 .
.
В частности, индуктивность бесконечно длинного соленоида (катушки) и тороида сечением 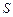 с числом витков
с числом витков 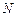 и длиной
и длиной 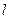
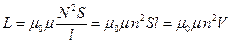 , (15.7)
, (15.7)
где 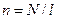 - число витков на единицу длины,
- число витков на единицу длины, 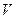 - объем соленоида (тороида).
- объем соленоида (тороида).
ЭДС самоиндукции можно выразить через напряжение на индуктивности 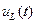 :
:
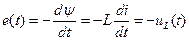 ,
, 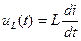 , (15.8)
, (15.8)
Изменение магнитного потока (15.4), пронизывающего замкнутый контур, может происходить по нескольким причинам. Назовем некоторые из них.
Во-первых, вследствие изменения индукции 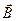 магнитного поля, что наблюдалось в опытах Фарадея.
магнитного поля, что наблюдалось в опытах Фарадея.
Во вторых, при повороте контура в постоянном магнитном поле, т.е. при изменении угла 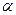 . Это наблюдается в электрогенераторах.
. Это наблюдается в электрогенераторах.
В третьих, вследствие перемещения контура или его частей в постоянном магнитном поле 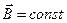 .
.
Рассмотрим возникновение ЭДС индукции в прямоугольном проводящем контуре, помещенном в однородное магнитное поле 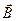 , перпендикулярное плоскости контура. Пусть одна из сторон контура длиной
, перпендикулярное плоскости контура. Пусть одна из сторон контура длиной 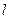 скользит со скоростью
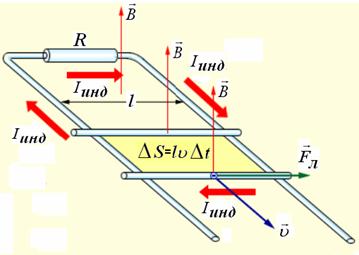
скользит со скоростью 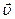 по двум другим направляющим сторонам (рис. 15.3).
по двум другим направляющим сторонам (рис. 15.3).
|
| Рис. 15.3 |
За время 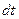 площадь контура изменяется на
площадь контура изменяется на 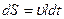 , что соответствует изменению магнитного потока на
, что соответствует изменению магнитного потока на 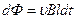 . Тогда ЭДС индукции
. Тогда ЭДС индукции
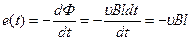 . (15.9)
. (15.9)
В рассмотренном случае модуль ЭДС индукции равен произведению скорости 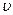 , магнитной индукции
, магнитной индукции 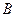 и длины
и длины 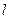 движущегося проводника.
движущегося проводника.
Полученное соотношение можно объяснить по-другому. На свободные заряды движущегося участка контура длиной 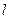 действует сила Лоренца, направленная вдоль проводника:
действует сила Лоренца, направленная вдоль проводника:
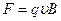 .
.
Под действием силы Лоренца свободные заряды перемещаются на расстояние 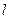 , при этом совершается работа
, при этом совершается работа 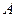 по перемещению заряда и возникает ЭДС индукции
по перемещению заряда и возникает ЭДС индукции 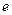
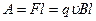 ,
, 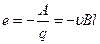 . (15.10)
. (15.10)
Если сопротивление проводящего прямоугольного контура равно 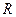 , то в контуре потечет ток
, то в контуре потечет ток
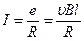 (15.11)
(15.11)
и выделится мощность
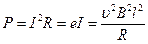 . (15.12)
. (15.12)
Заметим, что выделившаяся мощность образуется за счет источника ЭДС, создающего ток 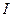 .
.
 2015-03-27
2015-03-27 732
732








