Симплексом называется правильный многогранник, имеющий n+1 вершину, где n – число факторов, влияющих на процесс. Так, если факторов два, то симплексом является правильный треугольник. Сущность симплексного метода оптимизации проиллюстрирована на рис.
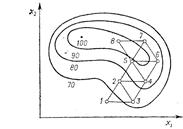
Рис. 3.1 – Оптимизация по симплексному методу
Начальная серия опытов соответствует вершинам исходного симплекса (точки 1,2 и 3). Условия этих первых опытов берутся из области значений факторов, соответствующих наиболее благоприятным из известных режимов оптимизируемого процесса.
Сравнивая между собой результаты опытов в точках 1, 2 и 3, находят среди них самый “плохой”, с точки зрения выбранного критерия оптимальности. Пусть, например, самым “неудачным” оказался опыт в точке 1. Этот опыт исключают из рассмотрения, а вместо него в состав симплекса вводят опыт в точке 4, которая симметрична точке 1 относительно противоположной стороны треугольника, соединяющей точки 2 и 3.
Далее сравнивают между собой результаты опытов в вершинах нового симплекса, отбрасывают самый “неудачный” из них и переносят соответствующую вершину симплекса в точку 5. Затем рассмотренная процедура повторяется в течение всего процесса оптимизации.
Если достигнут экстремум критерия оптимальности, то дальнейшее движение симплекса прекращается. Это значит, что новый шаг возвращает исследователя в предыдущую точку факторного пространства.
Следует иметь в виду, что симплексный метод, так же как и метод крутого восхождения, является локальным методом поиска экстремума. Если существует несколько экстремумов критерия оптимальности, то нужно осуществить их поиск, каждый раз, начиная оптимизацию из новой области факторного пространства. Затем следует сравнить между собой найденные оптимальные условия и из всех вариантов выбрать наилучший.
При оптимизации необходимо принимать во внимание ограничения, наложенные на влияющие факторы и функции отклика.
Важно отметить, что при пользовании симплексным методом не обязательно дублировать опыты. Дело в том, что ошибка в отдельном опыте может только несколько замедлить оптимизацию. Если же последующие опыты выполняются безупречно, то движение к оптимуму продолжается.
Матрица исходного симплекса в кодированных переменных представлена в табл. 3.1. Символом "0” обозначены координаты центра плана, т.е. основной уровень.
Таблица 3.1-Матрица исходного симплекса
| Номер опыта | х1 | х1 | … | х1 | х1 | Функция отклика |
| k1 | k1 | … | kn-1 | kn | y1 | |
| -R1 | k1 | … | kn-1 | kn | y2 | |
| 0 | -R2 | … | kn-1 | kn | y3 | |
| … | … | … | … | … | … | |
| n-1 | 0 | 0 | … | kn-1 | kn-1 | yn-1 |
| n | 0 | 0 | … | -Rn-1 | kn-1 | yn |
| n+1 | 0 | 0 | … | 0 | -Rn | yn+1 |
Очевидно, наибольшее количество опытов приходится ставить в начале эксперимента. Затем на каждом шаге оптимизации выполняется только один опыт.
Приступая к оптимизации, необходимо рассчитать матрицу исходной серии опытов в физических переменных, пользуясь формулой:
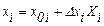 . (3.22)
. (3.22)
В дальнейшем все операции производятся только с физическими переменными.
Условия каждого нового опыта рассчитываются по формуле:
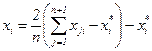 , (3.23)
, (3.23)
где n – число факторов в матрице планирования; j – номер опыта; i – номер фактора; хi* - значение i -го фактора в самом “неудачном” опыте предыдущего симплекса.
Следует отметить, что на любом шаге оптимизации, осуществляемой симплексным методом, можно включить в программу исследований новый фактор, который до тех пор не принимался во внимание, но оставался на постоянном уровне. При этом значения всех ранее рассматриваемых факторов рассчитываются по формуле:
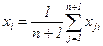 , (3.24)
, (3.24)
где i=1,2,…,n, т.е. являются средними арифметическими значениями соответствующих координат предыдущего симплекса.
Значение вновь вводимого фактора определяется по формуле:
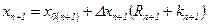 , (3.25)
, (3.25)
где
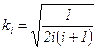 ;
;
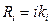
i – номер фактора в матрице планирования; 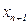 - основной уровень этого фактора;
- основной уровень этого фактора; 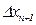 - выбранный шаг варьирования для данного фактора.
- выбранный шаг варьирования для данного фактора.
Отметим, что добавление нового фактора в состав полного факторного эксперимента сопровождается увеличением количества опытов вдвое. В этом смысле симплексный метод имеет очевидное преимущество.
 2015-03-27
2015-03-27 839
839








