2015-03-27
749
1. Основная задача теории транспортных сетей.
Определение 1: Транспортная сеть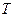 
есть совокупность двух объектов:
1. Связного графа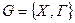 
, обладающего свойствами:
1°) в графе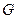 
отсутствуют петли,
2°) в графе 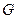существует одна и только одна вершина 
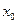такая, что множество 
,
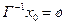3°) в графе 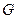существует одна и только одна вершина 
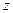, такая, что множество 
.
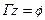2. Целочисленной неотрицательной функции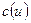 
, заданной на множестве 
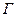дуг графа .
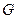Вершина 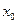называется входом сети, вершина 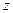— выходом. Значение функции 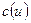на дуге 
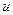называется пропускной способностью дуги.
Определение 2: Пусть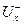 
— множество дуг, заходящих в вершину 
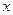, a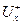 
— множество дуг, выходящих из вершины 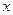. Целочисленная неотрицательная функция 
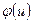, заданная на множестве 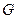дуг графа 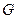, называется потоком, если она удовлетворяет следующим свойствам:
1) 
,
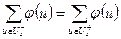
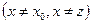2) 
.
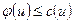Термины, входящие в определения 1 и 2, наводят на мысль, что при рассуждениях относительно транспортных сетей очень удобно представлять, что по дугам транспортной сети движется некоторая несжимаемая «жидкость». Дуги могут пропускать «жидкость» только в одном направлении и в количестве, не превышающем их пропускной способности. Свойство 1) определения 2 можно понимать как закон сохранения количества жидкости. Вся жидкость, движущаяся по транспортной сети, вытекает из входа сети и стекает в выход. Сколько жидкости поступает из входа сети, столько же стекает в выход, так как из свойства 1) определения 2 следует равенство:
|
|
|
.
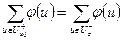Определение 3: Величина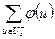 
называется величиной потока 
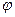и обозначается 
.
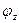Задача. На данной транспортной сети 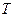построить поток наибольшей величины.
Прежде чем изложить алгоритм решения задачи, введем еще два термина. Дуга 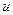называется насыщенной, если 
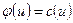. Поток 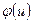называется полным, если каждый путь из вершины 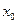в вершину 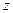содержит хотя бы одну насыщенную дугу.
