Прежде всего, заметим, что реализация алгоритма состоит из конечного числа шагов. В самом деле, п. 3° может применяться лишь конечное число раз, так как на каждом шаге величина потока увеличивается, по крайней мере, на единицу. Вместе с тем величина любого потока не может превзойти суммарной пропускной способности дуг, инцидентных выходу сети 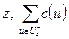 .
.
Процесс присвоения меток в силу того, что каждый раз получают метку еще неотмеченные вершины, конечен. И, наконец, в п. 5° поток 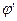 обладает большей величиной, чем
обладает большей величиной, чем 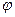 . Это вытекает из того, что по определению вершины
. Это вытекает из того, что по определению вершины 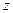 и правил п. 4° б) дугам, входящим в
и правил п. 4° б) дугам, входящим в 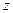 , может быть присвоен только знак «+».
, может быть присвоен только знак «+».
Получаемая по правилу 3° функция 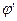 — поток. Это непосредственно следует из того, что
— поток. Это непосредственно следует из того, что 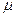 — путь. В соответствии с правилом п. 5° строится также поток. Чтобы доказать это утверждение, рассмотрим три соседние вершины последовательности
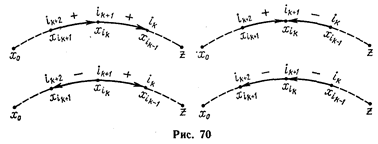
— путь. В соответствии с правилом п. 5° строится также поток. Чтобы доказать это утверждение, рассмотрим три соседние вершины последовательности 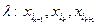 . В силу правила 4° б) возможны только ситуации, представленные на рис. 10. Но в этих ситуациях
. В силу правила 4° б) возможны только ситуации, представленные на рис. 10. Но в этих ситуациях 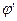 — поток.
— поток.
Пусть процесс, описанный в п. 4° б), приводит к тому, что вершина 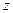 не получает метки. Обозначим через
не получает метки. Обозначим через 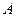 множество непомеченных вершин. В силу того, что
множество непомеченных вершин. В силу того, что 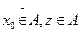 , множество
, множество 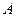 определяет разрез сети
определяет разрез сети 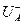 . Каждая дуга
. Каждая дуга 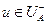 соединяет помеченную вершину
соединяет помеченную вершину 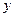 с непомеченной вершиной
с непомеченной вершиной 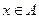 . Вершина
. Вершина 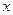 может остаться непомеченной при условии, что
может остаться непомеченной при условии, что 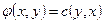 . Аналогично, на каждой дуге
. Аналогично, на каждой дуге 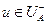 (выходящей из
(выходящей из 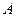 ) выполняется равенство
) выполняется равенство 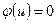 , поэтому справедливы соотношения:
, поэтому справедливы соотношения:
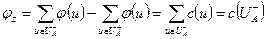 .
.
В силу леммы это означает, что поток 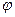 обладает наибольшей величиной.
обладает наибольшей величиной.
|
Проведенное рассуждение совместно с леммой составляют доказательство следующей теоремы.
Теорема 1: Для заданной транспортной сети величина наибольшего потока равна наименьшей пропускной способности разрезов, т. е. 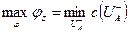 .
.
|
В качестве примера применения алгоритма Форда - Фалкерсона рассмотрим транспортную сеть  и полный поток
и полный поток 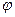 , для которого
, для которого 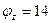 (рис. 11). Применяя правила 4° и 5° алгоритма, можно получить поток с величиной
(рис. 11). Применяя правила 4° и 5° алгоритма, можно получить поток с величиной 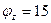 .
.
3. Задача о назначении на должность (комбинаторная прикладная задача).
Пусть в некотором учреждении имеется 6 вакантных должностей 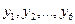 и 6 работников
и 6 работников 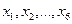 .
.
|
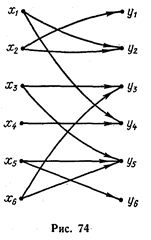
Граф 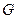 , изображенный на рис. 12, иллюстрирует, какие должности
, изображенный на рис. 12, иллюстрирует, какие должности 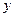 может в силу своей квалификации занимать работник
может в силу своей квалификации занимать работник 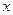 . Пусть выполнено условие: каждый работник может занимать хотя бы одну должность и на каждую должность претендует хотя бы один работник. Можно ли произвести назначение на должности так, чтобы все шесть должностей заняли работники соответствующей квалификации?
. Пусть выполнено условие: каждый работник может занимать хотя бы одну должность и на каждую должность претендует хотя бы один работник. Можно ли произвести назначение на должности так, чтобы все шесть должностей заняли работники соответствующей квалификации?
Один из способов решения этой задачи состоит в рассмотрении вспомогательной транспортной сети 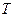 . Для ее получения добавим к множеству
. Для ее получения добавим к множеству 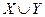 вершин графа
вершин графа 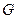 еще две вершины: вход
еще две вершины: вход 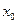 и выход
и выход 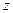 . Соединим
. Соединим 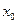 с каждой вершиной
с каждой вершиной 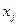 дугой пропускной способности
дугой пропускной способности 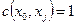 и каждую вершину
и каждую вершину 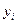 с
с 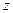 дугой пропускной способности
дугой пропускной способности 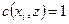 . Припишем дугам исходного графа
. Припишем дугам исходного графа 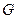 бесконечные пропускные способности. Получим транспортную сеть
бесконечные пропускные способности. Получим транспортную сеть 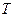 , изображенную на рис. 13.
, изображенную на рис. 13.
|
Ясно, что если на сети 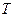 будет существовать поток такой, что
будет существовать поток такой, что 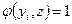 , то есть поток, насыщающий выходные дуги (одновременно он будет насыщать и входные дуги
, то есть поток, насыщающий выходные дуги (одновременно он будет насыщать и входные дуги 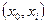 ), то требуемое назначение будет возможно произвести. Нужно назначить работника
), то требуемое назначение будет возможно произвести. Нужно назначить работника 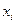 на должность
на должность 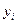 в том и только том случае, когда
в том и только том случае, когда 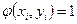 .
.
 2015-03-27
2015-03-27 581
581








