Пусть  – изолированная особая точка однозначной аналитической в области
– изолированная особая точка однозначной аналитической в области 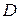 функции
функции  . Рассмотрим интеграл от этой функции по произвольному замкнутому контуру
. Рассмотрим интеграл от этой функции по произвольному замкнутому контуру 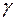 , лежащему в области
, лежащему в области 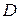 и содержащему внутри единственную особую точку
и содержащему внутри единственную особую точку  функции
функции  . Условия интегральной теоремы Коши в этом случае не выполнены, значит,
. Условия интегральной теоремы Коши в этом случае не выполнены, значит, 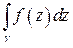 может быть отличен от нуля. Иначе: разделим контур
может быть отличен от нуля. Иначе: разделим контур 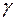 на две части произвольными точками
на две части произвольными точками 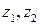 так, что из точки
так, что из точки 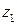 в точку
в точку 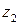 можно идти двумя различными путями
можно идти двумя различными путями 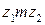 и
и 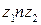 . Разность интегралов
. Разность интегралов
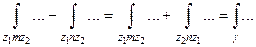
вообще говоря, не обязательно равна нулю. Возникает понятие вычета.
Определение.Вычетом функции  в точке
в точке  называется комплексное число, равное значению интеграла
называется комплексное число, равное значению интеграла 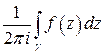 . Здесь
. Здесь 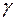 – произвольный замкнутый контур в области
– произвольный замкнутый контур в области 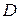 , охватывающий единственную особую точку
, охватывающий единственную особую точку  функции
функции  (контур обходится в положительном направлении).
(контур обходится в положительном направлении).
Вычет функции  в точке
в точке  обозначается символом
обозначается символом 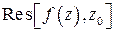 или
или 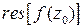 (от лат. residuum – вычет):
(от лат. residuum – вычет):
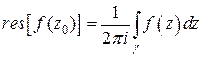 .
.
Пример 1. Показать, что вычет функции  в точке
в точке  равен коэффициенту при минус первой степени в лорановском разложении
равен коэффициенту при минус первой степени в лорановском разложении  в окрестности
в окрестности  .
.
Решение. Пусть  – изолированная особая точка функции
– изолированная особая точка функции  . Запишем соответствующее лорановское разложение:
. Запишем соответствующее лорановское разложение:
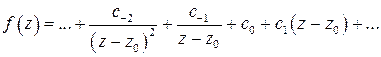 . (1)
. (1)
Возьмем произвольный контур 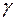 , охватывающий точку
, охватывающий точку  и расположенный в кольце сходимости ряда (1). Почленно проинтегрируем равномерно сходящийся ряд (1) вдоль контура
и расположенный в кольце сходимости ряда (1). Почленно проинтегрируем равномерно сходящийся ряд (1) вдоль контура 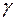 в положительном направлении. В примере 2 п.2 было показано, что если точка
в положительном направлении. В примере 2 п.2 было показано, что если точка  находится внутри контура
находится внутри контура 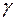 , то
, то
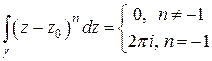 .
.
Значит, справа остается только одно слагаемое:
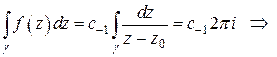
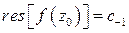 . ☻
. ☻
Задача 1. Показать, что вычет в устранимой особой точке равен нулю.
Вычет функции в изолированной особой точке  может быть отличен от нуля только для полюса или существенно особой точки, и то при условии, что
может быть отличен от нуля только для полюса или существенно особой точки, и то при условии, что 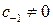 .
.
Задача 2. Показать, что вычет функции 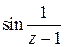 в точке
в точке 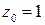 равен 1.
равен 1.
Пример 2. Найти вычет функции 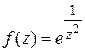 в точке
в точке 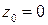 . Вычислить интеграл
. Вычислить интеграл 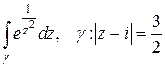 .
.
Решение. Запишем лорановское разложение функции 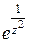 в окрестности существенно особой точки
в окрестности существенно особой точки 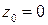 :
: 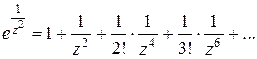 . Так как коэффициент
. Так как коэффициент 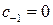 , то
, то 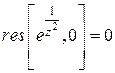 . Это следует и из четности функции
. Это следует и из четности функции  =
= 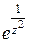 . В круге
. В круге 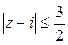 точка
точка 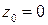 является единственной особой точкой функции
является единственной особой точкой функции  .
.
По определению вычета 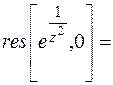
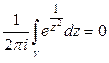 . ☻
. ☻
Задача 3. С помощью лорановского разложения показать, что в двукратном полюсе 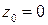 вычет функции
вычет функции 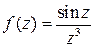 равен нулю.
равен нулю.
Пусть функция  в точке
в точке  имеет простой полюс, тогда
имеет простой полюс, тогда

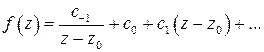 . (2)
. (2)
Чтобы найти вычет функции в точке  (коэффициент
(коэффициент 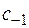 ), умножим обе части разложения (2) на
), умножим обе части разложения (2) на 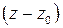 :
:
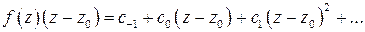 .
.
Переходя к пределу при 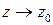 , получаем формулу для вычисления вычета в простом полюсе:
, получаем формулу для вычисления вычета в простом полюсе:
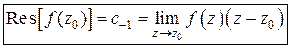 . (3)
. (3)
Пример 3. Найти вычет функции 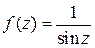 в точке
в точке 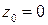 .
.
Решение. Так как для функции 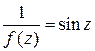 точка
точка 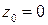 является простым нулем, то для функции
является простым нулем, то для функции 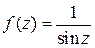 это простой полюс. Поэтому по формуле (3) находим
это простой полюс. Поэтому по формуле (3) находим 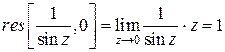 . ☻
. ☻
Задача 4. Найти вычеты функции 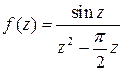 в ее особых точках.
в ее особых точках.
Ответ: 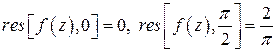 .
.
Пусть функция  в точке
в точке  имеет полюс
имеет полюс 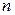 -го порядка, тогда
-го порядка, тогда
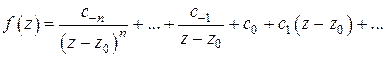 . (4)
. (4)
Сначала умножим обе части разложения (4) на 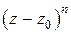 :
:
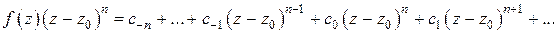
Чтобы найти коэффициент 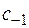 , надо почленно продифференцировать это разложение
, надо почленно продифференцировать это разложение 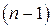 раз и перейти к пределу при
раз и перейти к пределу при 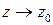 .
.
Получим формулу для вычисления вычета в 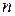 -кратном полюсе:
-кратном полюсе:
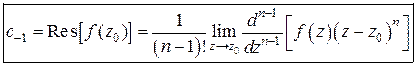 . (5)
. (5)
Пример 4. Найти вычеты функции 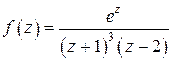 в ее особых точках.
в ее особых точках.
Решение. Данная функция имеет две особые точки: 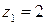 (простой полюс) и
(простой полюс) и 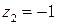 (трехкратный полюс).
(трехкратный полюс).
Для точки 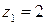 по формуле (3) находим:
по формуле (3) находим:
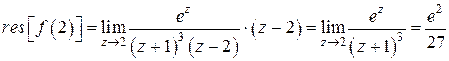 .
.
Для точки 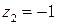 по формуле (5), полагая там
по формуле (5), полагая там 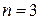 , получим
, получим
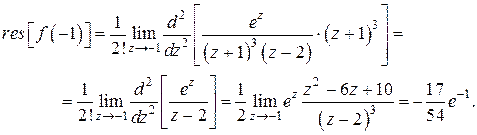 ☻
☻
Задача 5. Найти вычеты функции 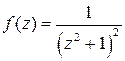 в ее особых точках.
в ее особых точках.
Ответ: 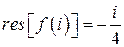 ,
, 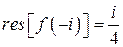 .
.
Задача 6. Пусть функция 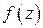 , имеющая в точке
, имеющая в точке  простой полюс, в окрестности точки
простой полюс, в окрестности точки  представляется как частное двух аналитических функций:
представляется как частное двух аналитических функций: 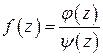 , где
, где 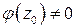 ,
, 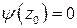 , но
, но 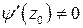 (то есть в точке
(то есть в точке  функция
функция 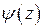 имеет простой нуль). Покажите, что формула (3) в этом случае принимает вид
имеет простой нуль). Покажите, что формула (3) в этом случае принимает вид
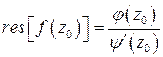 . (6)
. (6)
Указание. Воспользоваться определением производной функции 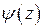 в точке
в точке  :
: 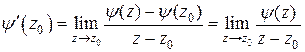 .
.
Пример 5. Вычислить 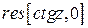 .
.
Решение. Для функции 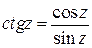 точка
точка 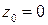 является простым полюсом (простым нулем для знаменателя
является простым полюсом (простым нулем для знаменателя 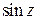 ).
).
Полагая в формуле (6) 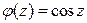 ,
, 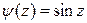 , получаем
, получаем
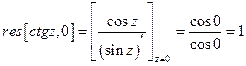 .☻
.☻
Интеграл от аналитической функции 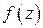 по замкнутому контуру
по замкнутому контуру 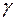 , содержащему внутри изолированные особые точки данной функции, помогает вычислить
, содержащему внутри изолированные особые точки данной функции, помогает вычислить
Основная теорема о вычетах. Пусть 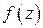 является аналитической в области
является аналитической в области 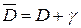 , за исключением конечного числа особых точек
, за исключением конечного числа особых точек 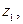
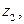 …
… 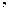
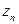 . Тогда
. Тогда
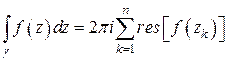 . (7)
. (7)
Пример 6. Вычислить интеграл 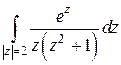 .
.
Решение. В круге 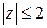 подынтегральная функция
подынтегральная функция 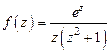 имеет простые полюсы в точках
имеет простые полюсы в точках 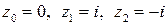 . По формуле (7) запишем:
. По формуле (7) запишем:
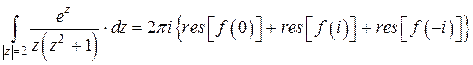 .
.
С помощью формулы (6) вычислим каждое слагаемое:
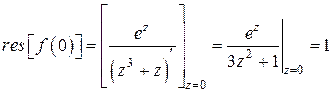 ;
;
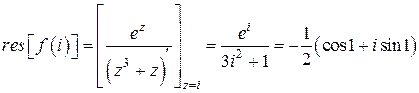 ;
;
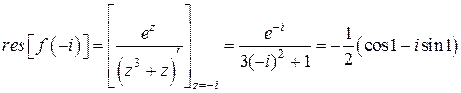 .
.
Сумма всех вычетов равна 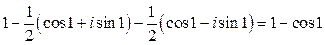 .
.
Значит, 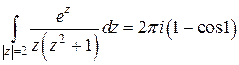 . ☻
. ☻
Задача 6. Показать, что 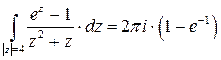 .
.
Определение. Вычетом функции 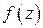 в бесконечно удаленной точке называется число, равное значению интеграла
в бесконечно удаленной точке называется число, равное значению интеграла 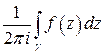 , взятому в отрицательном направлении (по часовой стрелке) вдоль границы окрестности точки
, взятому в отрицательном направлении (по часовой стрелке) вдоль границы окрестности точки 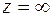 .
.
Задача 7. Показать, что в бесконечно удаленной точке вычет функции 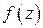 равен взятому с противоположным знаком коэффициенту при минус первой степени в лорановском разложении этой функции в окрестности точки
равен взятому с противоположным знаком коэффициенту при минус первой степени в лорановском разложении этой функции в окрестности точки 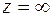 :
:
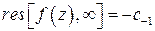 .
.
Если функция 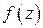 в бесконечно удаленной точке имеет устранимую особенность, то
в бесконечно удаленной точке имеет устранимую особенность, то 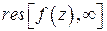 не обязательно равен нулю.
не обязательно равен нулю.
Пример 7. Найти вычет функции 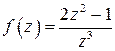 в точке
в точке 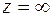 .
.
Решение. Так как 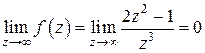 , то заданная функция в бесконечно удаленной точке имеет устранимую особенность. Представим функцию в виде
, то заданная функция в бесконечно удаленной точке имеет устранимую особенность. Представим функцию в виде 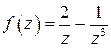 , здесь
, здесь 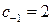 . Значит,
. Значит, 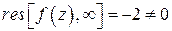 . ☻
. ☻
Задача 8. Показать, что 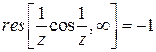 .
.
Вычет функции в бесконечно удаленной точке помогает также находить
Теорема. Пусть 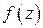 – аналитическая и однозначная в полной комплексной плоскости функция, за исключением конечного числа изолированных особых точек
– аналитическая и однозначная в полной комплексной плоскости функция, за исключением конечного числа изолированных особых точек 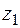 ,...,
,..., 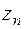 и точки
и точки 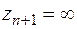 . Тогда сумма вычетов функции относительно всех этих точек равна нулю:
. Тогда сумма вычетов функции относительно всех этих точек равна нулю:
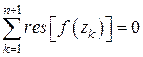 . (8)
. (8)
Пример 8. Найти 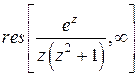 .
.
Решение. Сумма вычетов функции 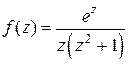 в особых точках
в особых точках 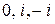 найдена в примере 6 и равна
найдена в примере 6 и равна 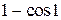 . В силу формулы (8) запишем
. В силу формулы (8) запишем
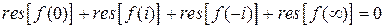
Значит, 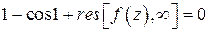 . Отсюда следует, что
. Отсюда следует, что
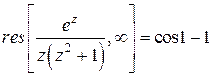 . ☻
. ☻
Пример 9. Пользуясь соотношением (8), вычислить интеграл 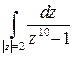 .
.
Решение. Подынтегральная функция 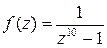 в круге
в круге 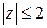 имеет десять изолированных особых точек
имеет десять изолированных особых точек 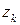 , расположенных на единичной окружности
, расположенных на единичной окружности 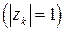 . В силу соотношения (8) и основной теоремы о вычетах имеем
. В силу соотношения (8) и основной теоремы о вычетах имеем
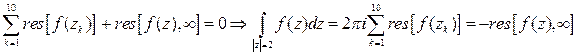 .
.
Но вычет четной функции 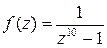 в бесконечно удаленной точке равен нулю, поэтому и
в бесконечно удаленной точке равен нулю, поэтому и 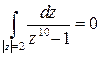 . ☻
. ☻
 2015-03-27
2015-03-27 5330
5330








